Groupe alterné - Définition
La liste des auteurs de cet article est disponible ici.
Groupe simple
Simplicité et groupe alterné
Une propriété éventuelle et importante d'un groupe est d'être simple, ce qui signifie qu'il ne contient pas de sous-groupe distingué propre.
-
- Si n est un entier supérieur ou égal à 5, le groupe alterné de degré n est simple.
Les groupes alternés forment une deuxième série infinie de groupes simples, après ceux, abéliens et d'ordre un nombre premier. Cette série contient le plus petit groupe simple non commutatif :
-
- Le groupe alterné de degré 5 est le plus petit groupe simple non abélien et tout groupe simple d'ordre 60 est isomorphe à A5.
La structure de groupe alterné intervient par exemple dans la résolution d'une équation algébrique par radicaux, à travers la proposition suivante :
-
- Si n est un entier supérieur ou égal à 5, le seul sous-groupe distingué et propre de Sn est An.
-
- Si n est un entier supérieur ou égal à 5, le groupe alterné de degré n est simple :
La méthode proposée ici est peu technique et n'utilise pas les théorèmes de Sylow. Il existe d'autres démonstrations plus courtes, particulièrement pour n égal à 5 se fondant sur les théorèmes cités.
Dans un premier temps, démontrons le lemme suivant :
-
- Soit H un sous-groupe distingué du groupe alterné An. Si H n'est pas réduit à l'élément neutre, il contient un cycle d'ordre 3 :
- Puisque H n'est pas réduit à l'élément neutre, nous pouvons choisir dans H un élément σ distinct de l'élément neutre.
- Supposons tout d'abord que la décomposition en cycles de supports disjoints de σ ne contienne pas uniquement des cycles d'ordre 3. Montrons qu'il existe une partie E à 3 éléments de {1, 2,... n} telle que F, l'union de E et de σ(E), contienne exactement 4 éléments. S' il existe dans la décomposition de σ au moins un cycle (a1 a2 a3 a4...) d'au moins quatre éléments, il suffit de définir E comme égal à {a1, a2, a3}. S'il n'en existe pas, il n'existe que des cycles d'ordre 2 et 3. Puisque nous supposons que la décomposition de σ ne contient pas uniquement des cycles d'ordre 3, il existe au moins un cycle d'ordre 2, donc il en existe au moins deux (a1 a2) et (b1 b2), sinon la signature de σ serait égale à -1 et σ ne serait pas dans le groupe alterné. Il suffit alors de définir E comme égal à {a1, a2, b1}.
- Choisissons un cycle γ de support E. C'est un cycle de longueur 3 et, en particulier, une permutation paire. Le support de σγσ-1 est égal à σ(E) et est donc distinct du support E de γ, donc les permutations σγσ-1 et γ sont distinctes, donc σγσ-1γ-1 est distincte de l'élément neutre. D'autre part, σγσ-1γ-1 s'écrit encore comme le produit de σ par un conjugué de σ-1 dans An; comme H est un sous-groupe distingué de An, σγσ-1γ-1 appartient donc à H et, d'après ce qui précède, à H-{1}. Comme le support de γ-1 est E et que le support du produit de deux permutations est contenu dans la réunion de leurs supports, le support de σγσ-1γ-1 est inclus dans F. Puisque F n'a que quatre éléments et que σγσ-1γ-1 est une permutation paire distincte de l'élément neutre, σγσ-1γ-1 est soit un cycle d'ordre 3, soit un produit de deux transpositions à supports disjoints. Nous avons donc prouvé que si la décomposition canonique de σ n'est pas formée uniquement de cycles d'ordre 3, H comprend soit un cycle d'ordre 3, soit un produit de deux transpositions à supports disjoints.
- Supposons maintenant que σ ne contienne que des cycles d'ordre 3. S'il n'en contient qu'un, σ est un cycle d'ordre 3 et la proposition est démontrée. Sinon, σ contient au moins 2 cycles d'ordre 3, que l'on note (a1 a2 a3) et (b1 b2 b3). Si γ désigne la permutation composée des deux transpositions (a1 b1) et (a2 b2), le produit σγ-1σ-1γ est le produit de σ par un conjugué de σ-1 dans An, il est donc élément de H. Ce produit est une permutation composée des 2 transpositions : (a1 b1) et (a3 b3). (Pour le montrer, noter que σγ-1σ-1, étant le conjugué de γ-1 = γ par σ, est égal à (σ(a1) σ(b1)) (σ(a2) σ(b2)) = (a2 b2) (a3 b3).)
- Pour conclure, il suffit de montrer que si H contient une permutation π composée de 2 transpositions à supports disjoints (a1 a2)(b1 b2), alors H contient un cycle d'ordre 3. Comme n est supérieur ou égal à 5, il existe un élément c qui n'est pas dans le support des deux transpositions. On considère γ, la permutation alternée (a1 a2 c). Par exemple en notant que πγπ-1 est la conjuguée de γ par π et est donc égale à (π(a1) π(a2) π(c)) = (a2 a1 c) = γ-1, on voit que πγπ-1γ-1 est un élément de H égal au cycle γ-2 = γ = (a1 a2 c), ce qui permet de conclure.
Nous avons donc prouvé notre lemme, à savoir que si n est au moins égal à 5, tout sous-groupe distingué de An non réduit à l'élément neutre comprend au mois un cycle d'ordre 3. Une fois ce lemme établi, il suffit de prouver que le seul sous-groupe distingué de An qui comprenne un cycle d'ordre 3 est An lui-même. Puisque An est engendré par les cycles d'ordre 3, il suffit de prouver que si H est un sous-groupe distingué de An qui comprend un cycle d'ordre 3, H comprend tous les cycles d'ordre 3. Pour cela, on peut par exemple prouver que si n est au moins égal à 5, deux cycles d'ordre 3 sont toujours conjugués dans An (et non seulement dans Sn.) Soient (a b c) et (x y z) deux cycles d'ordre 3. On sait qu'il existe une permutation σ telle que (x y z) = σ (a b c) σ-1. Si la permutation σ est paire, notre argument est vrai. Sinon, choisissons dans {1, ... n} deux éléments u, v distincts de x, y et z (ce qui est possible puisque n est au moins égal à 5). En conjuguant l'égalité (x y z) = σ (a b c) par (u v), nous trouvons que (x y z) est le conjugué de (a b c) par la permutation paire (u v) σ, et notre argument est encore vrai.
(Remarque : même si n n'est pas supposé au moins égal à 5, il est encore vrai que le seul sous-groupe distingué de An qui comprenne un cycle d'ordre 3 est An lui-même. En effet, on prouve facilement que si γ1 et γ2 sont des cycles d'ordre 3 dans An, un au mois des deux cycles γ2 et γ2-1 est conjugué de γ1 dans An et non seulement dans Sn.)
-
- Le groupe alterné de degré 5 est le plus petit groupe simple non abélien :
Dans un premier temps, utilisons un théorème de Burnside stipulant qu'un groupe simple non abélien possède un ordre dont la décomposition en facteurs premiers contient au minimum 3 nombres premiers. Les seuls entiers inférieurs à 60 vérifiant cette propriété sont 30 et 42.
Un groupe de 30 éléments n'est jamais simple, les théorèmes de Sylow permettent de le démontrer. Le premier montre l'existence d'un sous-groupe d'ordre 5 et d'un autre d'ordre 3. Les sous-groupes d'ordre 5 ont pour intersection deux à deux l'élément neutre car tout élément non neutre d'un sous-groupe engendre l'intégralité du sous-groupe. Deux autres théorèmes de Sylow montrent que si a est le nombre de sous-groupes d'ordre 5, a est un diviseur de 6 congru à 1 modulo 5. Il existe deux valeurs possibles, 1 et 6. Supposons qu'il n'existe qu'un unique sous-groupe d'ordre 5, tout conjugué d'un élément d'ordre 5 est aussi un élément d'ordre 5, donc un élément du sous-groupe et le sous-groupe est distingué. S'il existe 6 sous-groupes d'ordre 5, le groupe entier contient 24 éléments d'ordre 5. On raisonne alors sur les sous-groupes d'ordre 3. Un raisonnement analogue montre que si b est le nombre de sous-groupes d'ordre 3, b divise 10 et est congru à 1 modulo 3. Il en existe donc soit 1 soit 10. S'il en existait 10, on trouverait 20 éléments d'ordre 3, ce qui est incompatible avec l'existence de 24 éléments d'ordre 5. Les deux uniques éléments d'ordre 3 et l'identité forme alors un sous-groupe distingué.
Un raisonnement analogue montre qu'un groupe d'ordre 42 n'est jamais simple. La lettre a désigne maintenant le nombre de sous-groupes d'ordre 7. On sait que a est un diviseur de 6 congru à 1 modulo 7. Il n'existe qu'un unique sous-groupe d'ordre 7, nécessairement distingué.
-
- Si n est un entier supérieur ou égal à 5, le seul sous-groupe distingué et propre de Sn est An :
Soit H un sous-groupe distingué de Sn. L'intersection de H et du groupe alterné est, soit le groupe alterné, soit l'élément neutre. En effet, le groupe alterné est simple et n'admet pas de sous-groupe distingué non trivial. L'ordre du groupe alterné est égal à la moitié de celui du groupe symétrique.
Si H contient le groupe alterné, comme son ordre divise celui du groupe symétrique (le théorème de Lagrange) et que le groupe alterné est la moitié de celui du groupe symétrique, H est soit le groupe alterné, soit le groupe symétrique. Si H ne contient pas le groupe alterné il ne peut pas contenir plus de deux éléments. En effet, soit a et b deux éléments non neutres de H, leur signature est impaire, leur produit est donc dans le groupe alterné et est l'élément neutre. On en déduit que b est l'inverse de a, le même raisonnement montre que a2 est aussi l'élément neutre, donc a est égal à b, ce qui montre bien qu'il n'existe au plus qu'un élément de H non neutre. Cet élément fait partie d'une classe de conjugaison ne contenant qu'un unique élément car H est distingué. La seule classe de conjugaison réduite à un élément est celle de l'élément neutre, ce qui montre que H est réduit à un élément.
Exemple
Si le groupe de Galois d'un polynôme irréductible sur un corps parfait comme Q, celui des nombres rationnels, n'est pas résoluble, alors les racines du polynômes ne s'expriment pas à l'aide de radicaux. Tel est le contenu de la version formulée par Evariste Galois et en langage moderne, du théorème d'Abel. Les exemples les plus simples s'obtiennent à l'aide d'équation du cinquième degré dont le groupe de Galois est le groupe symétrique S5. Un tel groupe ne contient qu'un unique sous-groupe distingué propre, son groupe alterné. Il n'est donc pas résoluble.
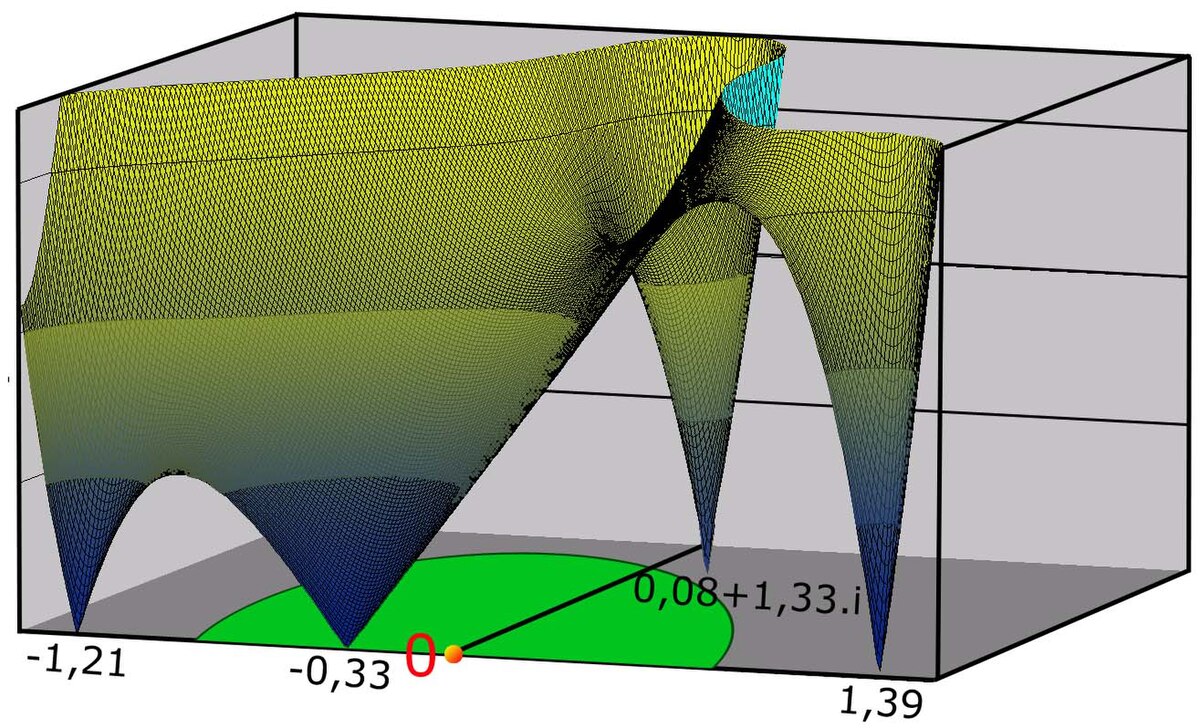
Le polynôme à coefficients dans Q : P(X) = X5 - 3X - 1 est un exemple de polynôme de cette nature, ce qui se démontre relativement simplement. Ce polynôme est illustré sur la figure de droite, plus précisément cette figure illustre la nappe qui à un nombre complexe z associe le module de P(z) pour les points de coordonnée imaginaire positive. On remarque que l'équation associée possède 5 racines dont trois réelles, de valeurs approximatives -1,21 -0,33 et 1,39 et deux imaginaires 0,08 + 1,33.i et son conjugué 0,08 - 1,33.i. Le fait qu'il n'existe qu'une unique racine dans le disque unité, illustré en vert sur la figure, montre que le polynôme est irréductible dans Q et que le groupe contient un élément d'ordre 5. L'existence d'un unique couple de racines imaginaires conjuguées montre l'existence d'une transposition dans le groupe. Ces deux propriétés établissent que le groupe de Galois est isomorphe à S5, qui n'est pas résoluble d'après les résultats précédents.
- Remarque 1 : Il est impropre de dire que l'équation P(z) = 0 n'est pas résoluble. Cette équation possède 5 racines qui s'approximent aussi précisément qu'on le souhaite et qui s'expriment exactement à l'aide d'intégrales elliptiques. En revanche, ces racines ne peuvent s'exprimer à l'aide des quatre opérations et de radicaux, ce qui démontre qu'il n'est pas possible de trouver une expression des racines dans le cas général d'une équation du cinquième degré, comme on peut le faire pour les équations de degré 1, 2, 3 ou 4.
- Remarque 2 : Les groupes simples non abéliens qui interviennent dans les groupes de Galois ne sont pas nécessairement des groupes alternés. Il existe ainsi un polynôme de degré 7 ayant pour groupe de Galois un groupe simple d'ordre 168. En revanche, si un polynôme de degré 5 n'est pas résoluble, cela signifie nécessairement que le groupe de Galois contient comme sous-groupe distingué le groupe alterné de degré 5.
-
- Le polynôme P(X) est irréductible dans Q[X] :
Montrons d'abord que le polynôme P(X) admet une unique racine dans le disque de centre 0 et de rayon 1. Pour s'en rendre compte, il suffit d'observer la figure de droite. Il est aussi possible de remarquer que si z parcourt le cercle unité des nombres complexes, la variable P(z) parcourt un tour autour de l'unité. En effet :
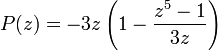
Le théorème des résidus montre l'existence et l'unicité d'une racine dans le disque unité.
Montrons ensuite que le polynôme P(X) admet exactement trois racines réelles. Pour cela, le théorème des valeurs intermédiaires ainsi que le calcul des valeurs du polynôme en -2, -1, 0 et 2 montre l'existence d'au moins trois racines réelles. La dérivée du polynôme, égale à 5X4 - 3, possède exactement deux racines, ce qui montre l'existence d'au plus trois racines réelles.
Le polynôme est irréductible. En effet, s'il ne l'était pas, il serait le produit de deux polynômes à coefficients dans Z car Z[X] est un anneau factoriel. Les deux coefficients dominants ainsi que les deux constantes de ces polynômes seraient égaux à 1. Ceci est contraire au fait que l'un des polynômes contient uniquement des racines de module strictement supérieur à 1.
-
- Le polynôme P(X) est irréductible dans Q[X] (seconde méthode) :
Une méthode plus manuelle consiste à rechercher les diviseurs possibles de P(X) dans Q[X]. Le caractère factoriel de l'anneau Z[X] montre que si le poynôme est réductible dans Q[X], il l'est aussi dans Z[X] (cf l'article Anneau factoriel). Le polynôme n'admet pas de racine entière, on en déduit qu'il n'existe pas de diviseur de degré 1 ou 4 dans Z[X].
Recherchons un diviseur de degré 2 ou 3. S'il en existe un, alors il existe deux entiers a et b, avec b=±1, tels que :
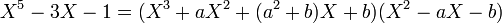
Le calcul du terme d'ordre 1 montre que a(a+1)=2b, c'est-à-dire b=1 et a=1 ou -2, ce qui est incompatible avec le calcul du terme d'ordre 2, a3+2ab-b=0.
On en déduit qu'il n'existe aucun diviseur de degré 2 ou 3 de P(X) dans Z[X], ce qui montre son irréductibilité dans Z[X].
-
- L'équation P(X) = 0 n'est pas résoluble par radicaux dans Q, l'ensemble des nombres rationnels :
Soit G le groupe de Galois du corps de décomposition K du polynôme. G opère sur les racines du polynôme, on en déduit que G s'identifie à un sous-groupe de S5 car les racines du polynôment engendre K, considéré comme une extension de Q. La conjugaison complexe est un automorphisme de K laissant invariant Q et permutant les deux racines complexes, on en déduit que G contient une transposition.
Montrons que G contient un élément d'ordre 5. Soit α une racine de P, le rapport entre l'ordre du groupe G et le cardinal du stabilisateur de α est égal au cardinal de l'orbite de α (cf Action de groupe (mathématiques)). Comme le polynôme P est irréductible, l'orbite de α est l'ensemble des 5 racines (cf Corps de décomposition). Ceci montre que l'ordre de G est un multiple de 5. Le théorème de Cauchy montre que G contient un élément d'ordre 5.
Montrons que G est isomorphe à S5. Les seuls éléments d'ordre 5 étant des cycles d'ordre 5, G en contient un. Or le groupe symétrique d'ordre 5 est engendré par tout couple composé d'une transposition et d'un élément d'ordre 5. Le groupe de Galois est en conséquence isomorphe à S5.
Le groupe de Galois contient un unique sous-groupe distingué propre A5. Ce sous-groupe est simple et non abélien, en conséquence, le groupe de Galois n'est pas résoluble. Le théorème d'Abel montre que l'équation polynomiale n'est pas résoluble par radicaux.