Groupe alterné - Définition
La liste des auteurs de cet article est disponible ici.
Groupe des rotations d'un polyèdre régulier
Représentation et géométrie
Les groupes A4 et A5 admettent des représentations de dimension 3 réelles. Ces représentations sont composées d'automorphismes qui peuvent être vus comme des isométries si l'espace vectoriel E de dimension 3 est équipé du bon produit scalaire. En effet, si G est le groupe des automorphismes, et (.|.) un produit scalaire quelconque de E, alors le produit scalaire <., .> suivant confère le statut d'isométrie aux éléments de G :
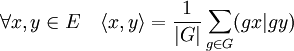
Ici, |G| désigne l'ordre du groupe G. Un élément de G est une isométrie car la translation à droite est une bijection. Ainsi, si h est un élément de G, l'ensemble des éléments g.h, si g décrit G, est exactement le groupe G.
Ces isométries sont tous des rotations car leur déterminant est égal à 1. Pour n égal à 4, il suffit de remarquer que la représentation est obtenue par restriction d'une représentation de S4, chacune des isométries est produit d'un nombre paire d'images de transpositions de déterminant égal à -1. Pour n égal à 5, la preuve est donné dans la construction de la table.
Les représentations de degré 3, pour n égal à 4 ou 5, sont fidèles, c'est-à-dire qu'elles sont injectives. Il suffit pour s'en persuader de remarquer que ces représentations possèdent des caractères qui prennent la valeur 3, que pour l'identité, l'image de l'élément neutre. Ces différentes propriétés permettent de concevoir ces représentations de dimension 3 comme des groupes de rotations d'un polyèdre régulier.
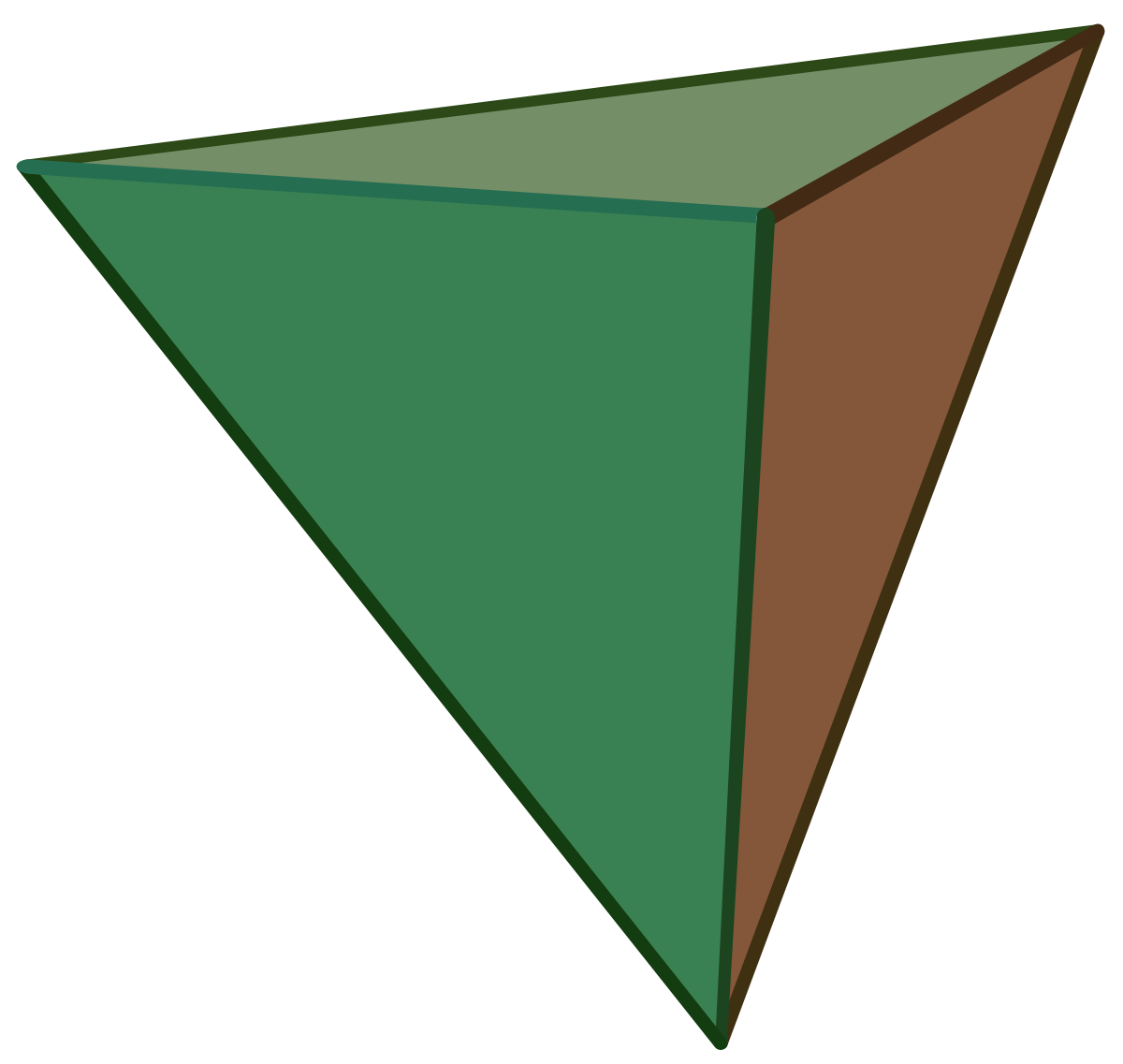
Groupe des rotations du tétraèdre
Si n est égal à 4, la représentation est obtenue en restreignant une représentation irréductible de degré 3 du groupe symétrique, décrite dans l'article Représentations du groupe symétrique d'indice quatre. Le groupe G est engendré par les deux automorphismes ayant les matrices suivantes dans une base orthonormale :
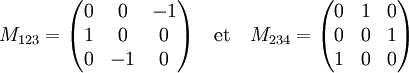
Soient φ234 l'automorphisme de matrice M234 et s un vecteur non nul de l'axe de la rotation φ234. On peut, par exemple choisir s comme le point de coordonnées (1, 1, 1). Soit S l'orbite de s, c'est-à-dire l'ensemble des points g(s), si g parcourt le groupe G. L'ensemble S est globalement stable par l'action de G. On définit le polyèdre comme l'enveloppe convexe de S, qui fournit les sommets du polyèdre recherché. Ce polyèdre est un tétraèdre régulier et son groupe des rotations est exactement égal à G.
-
- Le polyèdre contient 4 sommets :
La formule de Burnside (cf Action de groupe (mathématiques)) indique que le cardinal de S est égal à l'ordre de G que divise l'ordre du stabilisateur de s. Le stabilisateur de s est le sous-groupe de G composé des éléments laissant invariant s. Le stabilisateur contient au moins trois éléments : l'identité, φ234 et le carré de φ234. Il n'en contient pas d'autre. En effet, si g est un élément de G, différent d'une puissance de φ234 et admettant s comme point fixe alors le sous-groupe laissant s fixe est cyclique d'ordre strictement supérieur à 3. Un tel sous-groupe n'existe pas dans G. On en déduit que S est un ensemble à 4 éléments, c'est-à-dire : 12 l'ordre de G, que divise 3 l'ordre du stabilisateur de s.
-
- Le polyèdre est globalement invariant par l'action de G :
Le tétraèdre T, dont les sommets forment l'ensemble S, est globalement invariant par G. En effet, les sommets le sont, les arêtes le sont aussi car si s1 et s2 sont deux segments, l'image du segment [s1, s2] par un élément de G est un segment d'extrémités deux éléments de S. Le même raisonnement s'applique encore pour les faces et l'intérieur du polyèdre.
-
- Le polyèdre est régulier :
Le tétraèdre T est régulier. Pour s'en rendre compte, considérons un point quelconque t de S. Son orbite contient 4 éléments, donc son stabilisateur est d'ordre 3 et il existe une rotation φ de G, laissant invariant t. Il existe un vecteur s1 de S qui n'est pas dans l'axe dirigé par t. En effet, si tous les points de S étaient élément d'une droite vectoriel, cette droite seraient stable par G, la représentation ne serait pas irréductible car contiendrait un espace propre de dimension 1. Les trois points s1, φ(s1) et φ2(s1) forment avec t, l'ensemble S car il contient 4 éléments. Comme φ est une rotation d'axe dirigé par t, les trois points de S différents de t forment un triangle équilatéral. On en déduit que toutes les faces de T sont des triangles équilatéraux, ce qui montre que le tétraèdre T est régulier (ce qui signifie que les arêtes sont toutes de même longueur et que les angles de deux arêtes distinctes partageant un même sommet sont aussi tous égaux).
-
- Le groupe des rotations du polyèdre est exactement G :
Le groupe des rotations de T contient G, montrons maintenant qu'il est égal à G. Il existe 4 manière d'envoyer un sommet de S sur un autre sommet, car S contient 4 sommets. Il existe ensuite 3 manières de positionner une arête contenant le sommet s, sans bouger s. Le groupe des rotations de T ne peut donc contenir plus de 12 éléments. Comme G contient exactement 12 éléments, le groupe des rotations de T et G sont confondus.
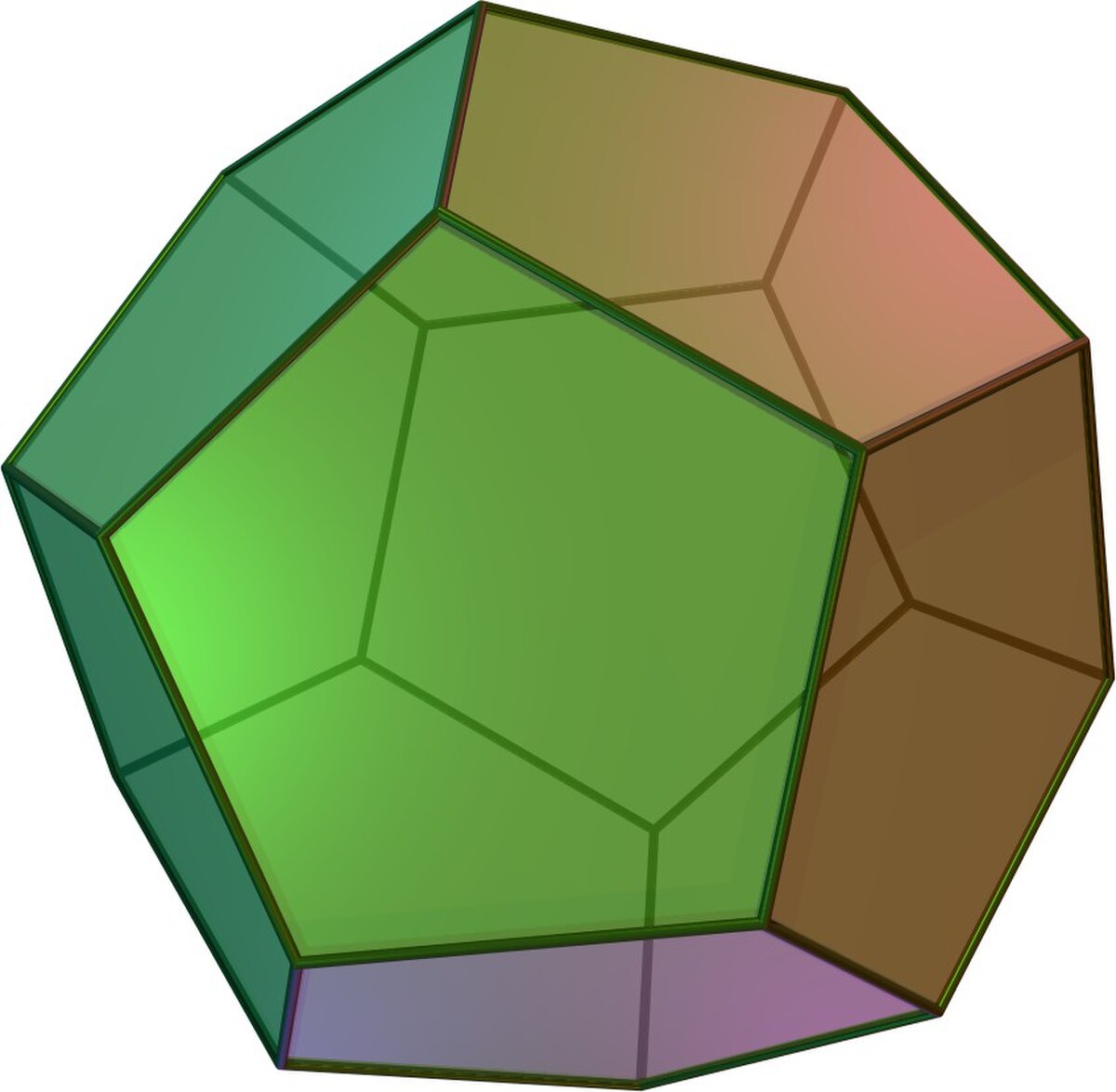
Groupe des rotations du dodécaèdre
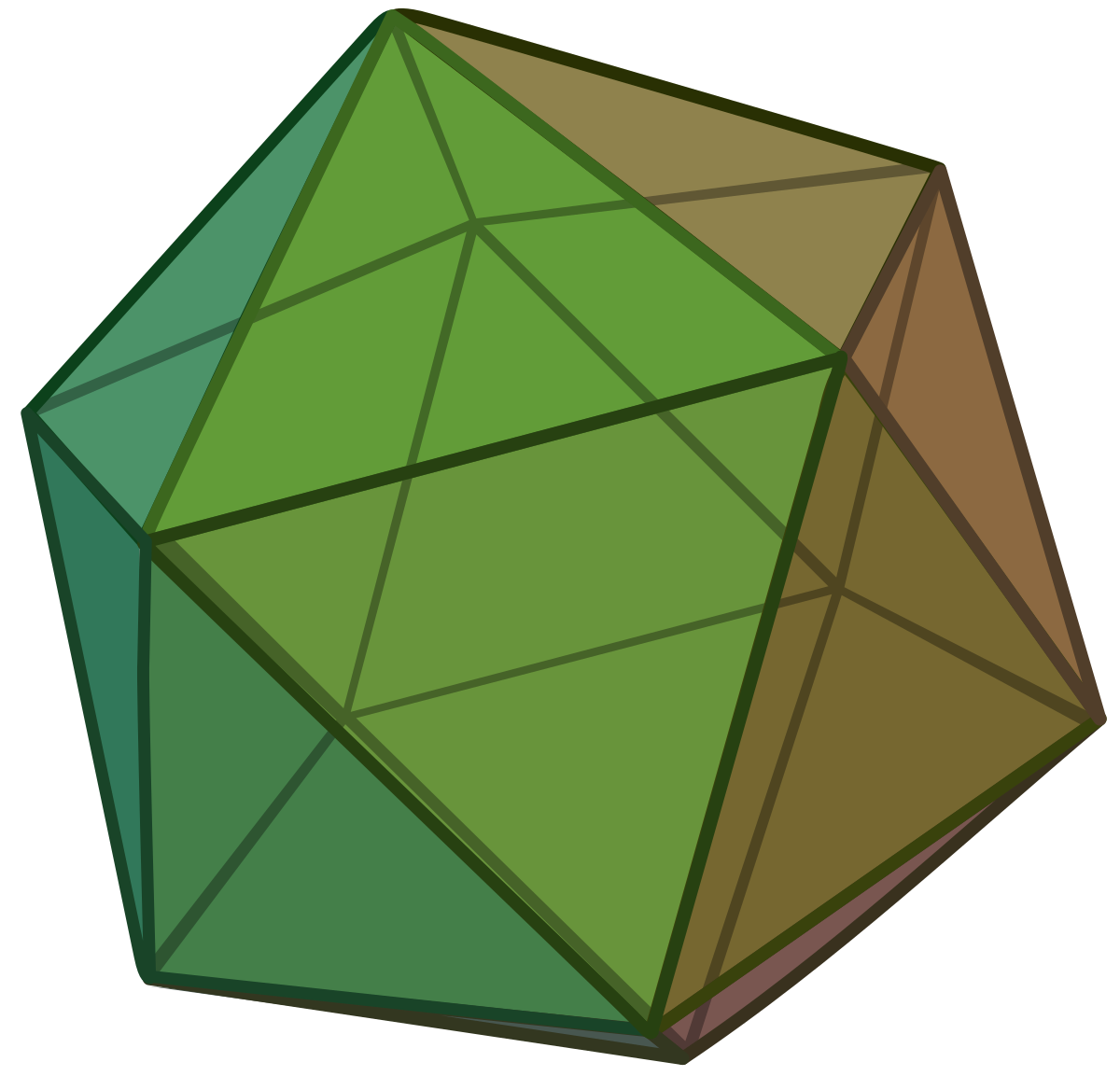
Le groupe A5 possède aussi une représentation irréductible d'ensemble d'arrivé G et de dimension 3. Un raisonnement, analogue à celui du paragraphe précédent, montre que le groupe des rotations d'un dodécaèdre régulier est isomorphe à G. Ceci revient à dire que le groupe des rotations du dodécaèdre régulier est isomorphe au groupe alterné de degré 5.
Le groupe G, qui laisse globalement invariant le dodécaèdre D laisse aussi globalement invariant l'ensemble des centres des faces du dodécaèdre. Le polyèdre, ayant pour sommets les centres des différentes faces de D, est un icosaèdre régulier. Il existe ainsi deux polyèdres réguliers ayant un groupe de rotations isomorphe à A5. La technique consistant à construire un nouveau polyèdre à partir des centres des faces est appelé polyèdre dual. Si un groupe d'isométries laisse invariant un polyèdre, le raisonnement utilisé ici montre qu'il laisse toujours invariant son dual.
Il existe deux manières de procéder. la première suppose connue la structure du dodécaèdre régulier et l'objectif est de montrer que son groupe des rotations est isomorphe à A5. Une méthode simple de procéder est de remarquer qu'il existe 5 cubes de sommets choisis parmi les sommets du dodécaèdre régulier. Le groupe des rotations opère librement sur l'ensemble de ces 5 cubes. Il est donc isomorphe à un sous-groupe de S5. On remarque ensuite que le groupe des rotations contient 60 éléments. En effet, comme le dodécaèdre contient 20 sommets, il existe 20 manières différentes de positionner un sommet. Une fois le sommet positionné, il reste encore trois manière de positionner une arête contenant ce sommet car chaque sommet est élément de trois arêtes. L'ordre du groupe des rotations est 20 que multiplie 3, c'est-à-dire 60. Un sous-groupe de 60 éléments dans S5 est nécessairement distingué car il peut être vu comme le noyau du morphisme qui associe 1 à un élément du sous-groupe et -1 aux autres éléments. Il n'existe qu'un unique sous-groupe distingué non trivial dans S5 c'est A5, ce qui montre l'isomorphisme recherché.
Une autre manière de procéder est d'utiliser la représentation de dimension 3 du groupe alterné pour construire le dodécaèdre et en déterminer ses paramètres. Elle est proposée dans la boîte déroulante.
L'objectif est de construire un solide de Platon ayant pour groupe de rotations G formé par les rotations d'une représentation irréductible de degré 3 de A5. Dans un premier temps, il est nécessaire de construire le polyèdre :
-
-
- Il existe un polyèdre convexe P à 12 sommets laissé globalement invariant par G :
-
- On procède comme pour le tétraèdre. Soit φ une rotation d'ordre 5 et s un vecteur propre de φ. On note S l'orbite de s par G, le même raisonnement que pour le tétraèdre montre que le stabilisateur de s est un groupe cyclique d'ordre 5 et que l'orbite est de cardinal 12. Il ne reste plus qu'à montrer que l'orbite de S n'est pas dans un plan. S'il l'était ce plan serait stable ou contiendrait une droite vectoriel stable par tout élément de G. Un tel sous-espace n'existe pas car les éléments de G proviennent d'une représentation irréductible. L'enveloppe convexe de S est un polyèdre P convexe globalement stable par G.
Il faut maintenant montrer que ce polyèdre est l'un des 5 solides de Platon. Pour cela, il suffit de montrer qu'il est régulier.
-
-
- Structure des arêtes autour d'un sommet :
-
- Soient t et s1 deux points distincts de S à une distance minimale d . L'orbite de t contient 12 points, son stabilisateur est, en conséquence, d'ordre 5 et il existe une rotation φ d'ordre 5 ayant pour axe celui dirigé par t. Les images de s1 par les puissances de φ forment un pentagone régulier situé sur un cercle C1 de centre l'intersection du plan contenant le pentagone et de l'axe de la rotation. Ce cercle ne contient pas d'autres points de S. Supposons en effet qu'il contienne un autre point u, il en contient au minimum 5 supplémentaires, formés par l'image de u par les puissances de φ. Il existerait alors au moins 10 points de S sur le cercle C1. Considérons le cercle C2 construit de la même manière , mais cette fois-ci à partir de s1 au lieu de t. Ce cercle contient au moins 5 points de S dont t et uniquement 2 peuvent être aussi des points de l'intersection de C1 et de S. Le cercle C2 contient au moins 2 points de S qui ne sont ni égaux à t ni dans C1. L'ensemble S contiendrait alors au moins 13 points : 10 dans C1, t et deux nouveaux dans C2. C'est absurde car S ne contient que 12 points.
- Il faut encore démontrer que s1 n'est pas dans la direction de t. Comme tous les points de S ont même norme, le seul point possible de S colinéaire est l'opposé -t. Or le point -t n'est pas un candidat pour être le point le plus proche de t. La sphère de rayon la norme de t et de centre le vecteur nul contient au moins 10 points de S, différents de t qui sont dans cette sphère et plus proches de t.
- Le segment [t, s1] est une arête, en effet, si s2 est l'image de s1 par φ et s5 son antécédent, les plans contenant t, s1, s2 pour le premier et t, s1, s5 pour le second, ne sont pas coplanaires.
- Tout point de S contient au moins 5 arêtes de longueur d dans le polyèdre. En effet, si v est un sommet quelconque de S, il existe une rotation de G qui envoie t sur v, car S est défini comme l'orbite de t. Cette rotation envoie s1 sur un point de S à une distance de d de v, le groupe des rotations de G laissant v invariant montre l'existence de 5 images par les éléments du groupe à situés à une distance d de v. Le caractère isométrique de la rotation montre que ce sont les seuls points de S à une distance inférieure ou égale à d de v.
Ce raisonnement montre l'existence de 30 arêtes dans le polyèdre, chaque point contient en effet 5 arêtes de longueur d, il existe 12 points dans S et chaque arrête contient 2 sommets, ce qui donne 12x5/2, soit 30 arêtes. Cependant rien ne garantit encore que ce sont les seules arêtes de P, on ne sait pas si [s1, s2] est de longueur d et si c'est une arête de P. Pour élucider cette question, étudions les faces du polyèdre.
-
-
- Structure des faces du polyèdre :
-
- Considérons les triangles de type t, s1, s2, c'est-à-dire formé par un point de S, un deuxième à distance d du premier et pour troisième l'image par une rotation d'axe t et d'angle un cinquième de tour. Comme la rotation est élément de G, s2 est bien un sommet de P. L'objectif est de montrer que ces triangles sont équilatéraux et forment les faces du polyèdre. Montrons qu'ils recouvrent le polyèdre, ou encore que tout point p de P est à une distance inférieure à d d'un sommet. Soit t le point le plus proche de p, s1, ..., s5 les 5 points de S à une distance d de t et C le cercle contenant ces 5 points. Les points à l'extérieur de la calotte sphérique de la sphère contenant S, délimité par le cercle C et contenant t, sont tous plus proches d'un des cinq points s1, ..., s5 que de t. On en déduit que p est dans la calotte, ce qui montre qu'il est dans un des triangles considérés.
- Soit ψ une rotation d'un tiers de tour de G. Son axe croise le polyèdre et donc un des triangles précédents, noté ici T. L'intersection c de l'axe et du triangle n'est pas un sommet du polyèdre car les sommets ont un stabilisateur d'ordre 5, qui ne contient aucun élément d'ordre 3. Soit s1 le point de S le plus proche de c. Les images de s1 par les rotations ψ et ψ2 sont deux points de S tout aussi proche de c que l'est s1. On en déduit que ces trois points sont les sommets de T, ce montre que T est équilatéral. Tout triangle de la famille précédente est isomorphe à T. En effet, soit T1 un des triangles, une isométrie transporte un des sommets de T1 sur l'un des sommets t de T, puis l'une des 5 rotations d'axe dirigé par t fait coïncider le triangle image avec T.
La structure du polyèdre est maintenant totalement élucidée. Si t est un sommet de S et s1, ..., s5 les 5 points de S à une distance d de t, [s1, s2] est bien une arête du polyèdre car sa longueur est égale à d. Les points s2, t s5 sont sur la même orbite pour le stabilisateur de s1 et l'on a démontré que les segments d'extrémités s1 et l'un des points de l'orbite, est une arête. On remarque qu'un sommet est partagé par 5 faces et que chaque face est partagé par 3 sommets, ce qui montre l'existence de 12x5/3 = 20 faces. Le polyèdre construit est bien un solide de Platon car il est régulier, on reconnaît d'ailleurs l'icosaèdre.
-
-
- Construction du dodécaèdre :
-
- Le dodécaèdre est le polyèdre dual de l'icosaèdre. Il est régulier et possède le même groupe de rotation G, comme tous les polyèdres duaux d'un polyèdre régulier. Ces sommets sont les centres des faces de l'icosaèdre, comme l'icosaèdre contient 20 faces, il possède 20 sommets. Le centre de chacune des faces se situe sur l'axe contenant le vecteur nul et un sommet de l'icosaèdre. Cet axe est celui d'une rotation d'ordre 5 de G, ce qui montre que chaque face est un pentagone dont le plan est orthogonal à l'axe de la rotation. De plus il existe autant de faces que l'icosaèdre contient de sommets, c'est-à-dire 12. Le dodécaèdre contient 20 sommets chacun centre d'une rotation d'ordre 3, chaque sommet contient donc 3 arêtes. Il existe 12 sommets, donc 20x3/2 = 30 arêtes.