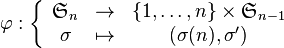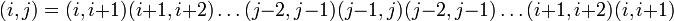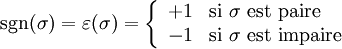Groupe symétrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
- Cette notion est différente de celle de groupe de symétrie.
En mathématiques, plus particulièrement en algèbre, le groupe symétrique d'un ensemble E est le groupe des permutations de E, c'est-à-dire des bijections de E sur lui-même.
Définition
Soit E un ensemble. On appelle groupe symétrique de E l'ensemble des applications bijectives de E sur E muni de la composition d'applications (la loi

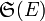
Un cas particulier courant est le cas où E est l'ensemble fini
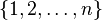
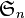
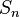
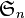
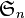
Maintenant, si

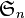
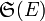
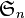
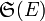
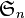
Origine et importance
Historiquement, l'étude du groupe des permutations des racines d'un polynôme par Évariste Galois est à l'origine du concept de groupe.
Un théorème de Cayley assure que tout groupe peut être considéré comme sous-groupe d'un groupe symétrique.
Propriétés issues de l'étude du groupe alterné
Le résultat fondamental dans l'étude du groupe alterné
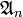
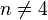
Il en résulte notamment que le groupe dérivé de
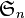
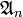
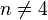
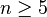
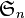
Propriétés
Le groupe
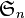
Cette propriété peut être prouvée en dénombrant les permutations. Il est également possible de faire une démonstration par récurrence, en donnant ainsi un lien entre les groupes symétriques d'ordre n-1 et n.
- Démonstration par récurrence sur n.
-
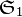
- Supposons que possède (n − 1)! éléments. Considérons l'application
-
- où σ' est la restriction à
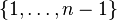
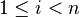
- On montre la bijectivité de

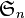
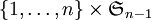
Le groupe symétrique est isomorphe au groupe formé par les matrices de permutation muni de la loi produit : ce sont les matrices ayant un unique coefficient 1 dans chaque ligne et chaque colonne, tous les autres étant nuls.
Générateurs du groupe symétrique
Une transposition est une permutation qui échange deux éléments et laisse les autres inchangés. On note par (i,j) la transposition qui échange l'élément i avec l'élément j.
Il existe un algorithme permettant de décomposer une permutation en produit de transpositions. Ainsi l'ensemble des transpositions forme un système de générateurs de
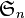
Il est possible de se limiter aux transpositions de la forme τi = (i,i + 1) puisque, pour i
Ces générateurs permettent de donner une présentation du groupe symétrique, avec les relations
-
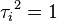
 ,
,-
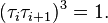
Il s'agit donc d'un cas particulier de groupe de Coxeter.
Il est possible également de prendre pour système de générateurs les transpositions de la forme (1,i) pour i>1. Enfin on peut se contenter de deux générateurs : la transposition σ=(1,2) et le cycle c=(1,2,...,n).
Signature
Toute permutation se décompose en un produit de transpositions. Ce produit n'est pas unique, mais le nombre de transpositions nécessaire pour représenter une permutation est toujours soit pair, soit impair. On parle alors de permutation paire ou impaire.
La signature d'une permutation σ est l'application notée sgn ou

Avec cette définition, la signature est un homomorphisme de groupes
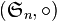
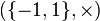
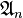
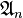
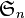
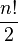

Classes de conjugaison
Si σ est une permutation, sa classe de conjugaison est l'ensemble des conjuguées de σ
Les conjuguées de σ sont les permutations dont la décomposition en produit de cycles à supports disjoints a la même structure que celle de σ : même nombre de cycles de chaque longueur.
Ainsi, si on considère dans
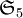
Les permutations (1,2,3)(4,5) et (1,3,4)(2,5) sont dans la même classe de conjugaison et la permutation (1,3)(2,5) non.
- Soient σ et φ deux permutations de
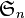
Un résultat précédent montre qu'il est possible de décomposer σ en une suite de transpositions : σ = σ1σ2...σm. L'objectif revient à montrer que σm-1σm-1-1...σ1-1φσ1σ2...σm a même structure que φ. Ceci revient à montrer que si σ est une transposition, alors σ-1φσ possède la même structure que φ. Soient a1 et b1 les deux éléments du support de σ, c'est-à-dire que σ(a1) = b1 et σ(b1) = a1. On peut diviser l'étude en quatre cas différents.
Si ni a1, ni b1 ne sont élément du support de φ, φ et σ commutent et σ-1φσ = φ, ce qui montre le résultat.
Si a1 est élément du support de φ, mais que b1 ne l'est pas. Soit (a1a2...ak) le cycle de φ contenant a1. Les cycles de σ-1φσ sont exactement les mêmes que ceux de φ, à l'exception de celui contenant a2, qui devient (b1a2a3...ak) et qui est un cycle de même longueur. Si b1 n'est plus invariant par σ-1φσ, a1 l'est devenu. Les deux permutations σ-1φσ et φ ont bien même structure.
Si a2 et b2 appartiennent au même cycle, avec les notations précédentes, il existe un entier h, plus petit que k tel que b2 soit égal à ah avec h différent de 2. Les différents cycles à supports disjoints composant φ sont les mêmes que ceux de σ-1φσ à l'exception de celui contenant a2, qui devient (a1aha3...ah-1a2ah+1ah+2...ak). Une fois encore les structures des cycles sont les mêmes.
Si a1 et b1 sont tout deux éléments du support de φ et appartiennent à des cycles différents, on note (b1b2...bl) le cycle de b1. Tous les cycles de φ restent inchangés, sauf ceux contenant a1 et b1, qui deviennent : (a1b2...bl) et (b1a2...ak). Les deux permutations ont encore la même structure.
- Soient φ1 et φ2 deux permutations ayant même structure. Il s'agit, pour clore la démonstration, de montrer l'existence d'une permutation σ tel que σ-1φ1σ = φ2.
Dans un premier temps, on construit une permutation σ1σ2...σk tel que σk-1σk-1-1...σ1-1φ1σ1σ2...σk ait même support que φ2. Soit b1, b2 ... bj les entiers compris entre 1 et n qui ne sont pas dans le support de φ2. Si bi, où i est un entier entre 1 et j, n'est pas dans le support de φ1 on définit σi comme la permutation identité et ci comme étant égal à bi. Dans le cas contraire, il existe nécessairement un élément ci élément de l'ensemble {b1, b2 ... bj} qui est dans le support de φ1 car φ1 et φ2 ont même structure et par conséquent même nombre d'éléments invariants. On peut, de plus choisir ci différent de cp pour p variant de 1 à i. Soit σi la transposition de support bi et ci, la permutation σi-1φ1σi laisse bi invariant. Par récurrence, on vérifie bien que σk-1σk-1-1...σ1-1φ1σ1σ2...σk possède le même support que φ2.
Dans un deuxième temps, on construit une permutation σ1σ2...σl, où l est un entier plus grand que k, tel que σl-1σl-1-1...σ1-1φ1σ1σ2...σl ait même support et même élément dans chaque cycle que φ2. Les différentes permutations σp sont définies jusqu'à l'indice k, il faut maintenant les définir jusqu'à l'indice l. Soit (a1a2...ap) un cycle de σk-1σk-1-1...σ1-1φ1σ1σ2...σk et (b1b2...bp) un autre cycle de même longueur de φ2. Si a1 est élément de {b1, b2, ..., bp) on définit σm+1 comme la permutation identité, sinon c'est la transposition de support a1 et b1. Le premier élément du cycle de longueur p et contenant b2 est maintenant commun à σk+1-1σk-1...σ1-1φ1σ1σ2...σk+1. De proche en proche on construit ainsi la permutation ayant même support et même élément dans chaque cycle.
Dans un troisième temps, on construit une permutation σ1σ2...σm, où m est un entier plus grand que l, tel que σm-1σm-1-1...σ1-1φ1σ1σ2...σm soit égal à φ2. Il devient nécessaire d'ordonner les éléments dans les différents cycles. Soit (a1a2...ap) un cycle de σl-1σl-1-1...σ1-1φ1σ1σ2...σl et (a1aψ(2)...aψ(p)) la permutation de même support dans φ2. Ici ψ désigne une permutation de {2, ..., p}. Si aψ(2) est égal à a2 alors σl+1 est la permutation identité. Sinon, σl+1 est la transposition de support a2 et aψ(2). L'image de a1 par la permutation σk+1-1σk-1...σ1-1φ1σ1σ2...σk+1 est bien celle de φ2. De proche en proche on construit la permutation recherchée.