Groupe alterné - Définition
La liste des auteurs de cet article est disponible ici.
Représentation
Caractère
Une manière d'étudier un groupe G est de le représenter à l'aide d'un sous-groupe d'un groupe linéaire. Le cas le plus simple est celui où le corps de l'espace vectoriel est celui des nombres complexes. Certaines représentations sont particulièrement digne d'intérêt, on les appelle les représentations irréductibles, elles ne possèdent pas de sous-espaces stables par la représentation autre que l'espace entier et celui réduit au vecteur nul.
Le caractère d'une représentation est l'application qui à un élément du groupe associe la trace de son endomorphisme. Si la représentation φ est irréductible, son caractère χφ est de norme 1, pour la norme définie par le produit hermitien suivant, où g est le cardinal du groupe G :
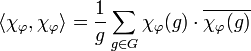
Les caractères de deux représentations irréductibles non isomorphes sont orthogonaux et si χi désignent les différents caractères des représentations irréductibles et e l'élément neutre du groupe G, alors :
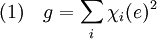
Groupe alterné de degré 4
Un premier caractère irréductible est donné par la représentation triviale t dans un espace de dimension 1. À chaque élément de A4 cette représentation associe l'automorphisme identité, le caractère χt de cette représentation associe 1 à chaque élément du groupe A4.
On obtient une deuxième représentation φ par restriction de la représentation φ1 de S4 aux éléments de A4, en utilisant les notations de l'article Représentations du groupe symétrique d'indice quatre. Comme la valeur d'un caractère ne dépend pas du choix d'un élément pris dans une même classe de conjugaison, le caractère est défini par χφ(e) = 3, χφ(ab)(cd) = -1 et χφ(abc) = 0. Un calcul montre que la norme de cette représentation est égale à 1, elle est donc irréductible.
Il existe un morphisme de A4 dans le groupe cyclique d'ordre 3. Il existe deux représentations irréductibles du groupe cyclique d'ordre 3 qui sont toutes deux de dimension 1. La première associe j, la racine cubique de l'unité de partie imaginaire strictement positive, à un élément d'ordre 3 et la deuxième associe son conjugué à la même valeur.
L'égalité (1) montre qu'il n'existe pas d'autre représentation irréductible, à un isomorphisme près. En effet, 32 + 12 + 12 + 12 est égal à 12, l'ordre du groupe alterné de degré 4. On en déduit la table des caractères :
|
Il existe une représentation de dimension 3. Elle est utilisée dans le paragraphe "Groupe des rotations du tétraèdre".
Groupe alterné de degré 5
Les caractères du groupe alterné de degré 5 sont un peu plus délicats à déterminer que le cas précédent, même s'il est possible d'y parvenir sans utiliser une approche générique plus lourde. L'existence de 5 classes de conjugaison montre qu'il existe 5 représentations irréductibles. La table des caractères est la suivante :
|
Les caractères de ces représentations sont tous réelles. Chacune de ces représentations s'incarne sur un espace vectoriel réel (cf Caractère d'une représentation d'un groupe fini). Cette remarque s'applique, en particulier, sur les représentations de dimension 3. Le paragraphe "Groupe des rotations du dodécaèdre" montre qu'une telle représentations correspond à un groupe de symétrie d'un solide de Platon.
Il n'existe pas de morphisme non trivial de A5 dans un groupe cyclique. En effet, le noyau d'un tel morphisme est un groupe distingué, c'est-à-dire soit l'élément neutre soit le groupe A5. Comme le groupe A5 n'est pas abélien, le morphisme ne peut être injectif et si le noyau n'est pas l'élément neutre, c'est le groupe entier. Cette remarque permet d'élucider rapidement la nature des représentations de degré 1 et 2.
-
-
- La seule représentation irréductible de degré 1 ou 2 est la représentation triviale :
-
- Une représentation de degré 1 est un morphisme de A5 dans un groupe cyclique sous-groupe des racines de l'unité des nombres complexes, la remarque précédente permet de conclure. Pour le degré 2, l'application qui à un élément de A5 associe le déterminant de sa représentation est aussi un morphisme à valeur dans un groupe cyclique sous-groupe des racines de l'unité des nombres complexes. Un tel déterminant est égal à 1, en dimension 2, cela signifie que les deux valeurs propres sont conjugués et que le caractère est à valeurs réelles. Une représentation dont le caractère est à valeurs réelles est réelle. Or en dimension 2, les seules isométries de déterminant égal à 1 sont les rotations. L'ensemble d'arrivé est encore un groupe cyclique, la représentation est encore triviale.
Il existe autant de représentations irréductibles que de classes de conjugaison. Dans le cas de A5 il en existe 5. Avoir déterminer les représentations de degré 1 et 2 permet de calculer la dimension de chacune de ces représentations.
-
-
- Les représentations irréductibles ont pour degré respectifs 1, 3, 3, 4 et 5 :
-
- L'égalité 1 montre que l'ordre de A5 est égal à la somme des carrés des différentes représentations irréductibles. Si l'on néglige la représentation triviale, la somme des carrés des différents degrés est égale à 59. Il suffit pour établir le résultat de déterminer le nombre de manière de décomposer 59 en somme de 4 carrés. Comme aucun carré ne peut être égal à 4, il n'existe qu'une unique possibilité 3, 3, 4 et 5.
-
-
- Le caractère de degré 4 est égal à (4, 0, 1, -1, -1) :
-
- Pour le construire, on utilise une technique analogue à celle de la représentation régulière. On fait opérer le groupe alterné sur une base de l'espace et on prolonge les applications obtenues par linéarité. Le caractère associé est (5, 2, 1, 0, 0). La représentation contient un espace propre de dimension 1 associé à la représentation triviale. Il correspond à la droite vectoriel dirigé par la somme des 5 éléments de la base. En retranchant cette représentation on obtient une nouvelle représentation dont le caractère est égal à la différence du caractère précédent et du caractère trivial, soit (4, 1, 0, -1, -1). Il suffit de vérifier que sa norme est égale à 1 pour conclure sur l'irréductibilité de la représentation associée.
-
-
- Calcul des deux caractères σ1 et σ2 de degré 3:
-
- Les éléments de la deuxième classe de conjugaison sont d'ordre 2, les valeurs propres associées sont nécessairement 1 ou -1, ce qui donne pour valeurs possibles du caractère : 3, 1, -1, -3. La norme du caractère est égal à 1, ce qui limite à 1 et -1 les valeurs possibles, puis comme le déterminant est égal à 1, on ne trouve que -1. Pour la troisième valeur, il suffit de calculer le produit scalaire du caractère avec la somme de ceux de degré 1 et 4, on trouve 0 pour les deux caractères. Si τ est une permutation dans une des deux dernières classes, τ et τ-1 sont éléments de la même classe, or les caractères de τ et celui de τ-1 sont conjugués, ce qui montre qu'ils sont réels. Le calcul de la norme montre que la somme des carrés des deux dernières valeurs du caractère est égale 3/2 et le produit scalaire avec le caractère trivial montre que leur somme est égale à 1. On trouve 1/2.(1 + √5) et 1/2.(1 - √5).
-
-
- Le caractère de degré 5 est égal à (5, 1, -1, 0, 0) :
-
- On connait le caractère de la représentation régulière et on sait qu'il est composé de p représentations irréductibles de degré p. On en déduit la valeur du dernier caractère.