Horizon cosmologique - Définition

Cas particuliers

Dans le cas où l'univers possède la densité critique et n'est composé que d'une espèce, dont le rapport de la pression à la densité d'énergie est w, on a

.

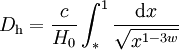
Cette intégrale peut être évaluée selon plusieurs cas

Univers de radiation (w = 1/3)

On a immédiatement

,

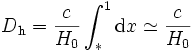
l'égalité ci-dessus étant une approximation car on n'a pas tenu compte de la valeur exacte de la borne inférieure (prise à 0 ici alors qu'elle pourrait être prise à une valeur légèrement positive). Dans ce cas, la taille de l'horizon correspond exactement au rayon de Hubble.

Univers de poussière (w = 0)

On a désormais

.

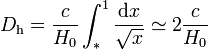
Dans ce cas, la taille de l'horizon correspond exactement au double du rayon de Hubble.

Univers à équation d'état constante

Plus généralement, on a, dans le cas où w est constant et supérieur à − 1 / 3,

.

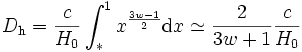
D'une manière générale, plus l'équation d'état est « dure » (c'est-à-dire w grand), plus la taille de l'horizon est faible en unité du rayon de Hubble. Ceci peut être rendu plus explicite en utilisant la relation existant entre âge de l'univers t₀et rayon de Hubble. Les équations de Friedmann indiquent que

.

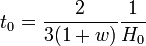
En combinant ces deux derniers résultats, il vient

.

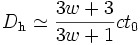
Ce résultat tend vers ct₀ quand w tend vers l'infini. Cela s'interprète par le fait que cette limite correspond en fait au cas idéalisé où la matière tend à être incompressible (une variation de pression arbitrairement grande donnant lieu à une petite variarion de densité, ce qui est le cas si P = wρ est grand car alors ). Dans ce cas, une telle matière a tendance à arrêter sa phase d'expansion le plus rapidement possible (elle s'oppose à une variation de son volume), ce qui fait que la phase d'expansion qui suit immédiatement le Big Bang s'arrête très vite, et que l'expansion tend à cesser. Dans un tel cas, on est dans une situation identique à celle de l'espace de Minkowski où au bout du temps t₀ on peut recevoir des signaux distants de ct₀. À noter cependant que le cas w > 1 est a priori physiquement irréaliste, car l'équation d'état est acausale : la vitesse du son dans un tel fluide, donnée par dépasse celle de la lumière. À l'inverse, l'intégrale diverge quand w tend vers la valeur -1/3 (voir ci-dessous).

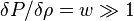
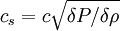
Univers de Milne (w = - 1/3)

L'univers de Milne correspond à un espace vide de matière. Dans ce cas, tous les paramètres de densité sont nuls, ce qui formellement, du point de vue des équations de friedmann, peut s'interpréter comme un univers ayant la densité critique et un paramètre d'équation d'état w égal à -1/3. Il vient

.

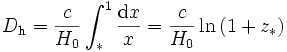
La primitive à calculer donne un logarithme. Il faut ici prendre soigneusement en compte la valeur de la borne inférieure. Si elle est nulle ( ), alors l'intégrale est infinie. Ce résultat tend à indiquer qu'il n'y a alors pas d'horizon, c'est-à-dire que toute région de l'univers est accessible à l'observation. Ceci peut se comprendre en remarquant que l'univers de Milne peut être vu comme une portion de l'espace de Minkowski, avec une origine d'où sont issues les particules fictives qui marquent l'expansion de l'univers en se déplaçant à vitesse constante (voir Univers de Milne). Dans un tel cas, toutes les lignes d'univers de ces particules fictives d'intersectent les unes les autres à l'origine et sont donc toutes dans le cône de lumière passé des unes et des autres, ce qui fait que la totalité de l'univers est nécessairement observable. Si par contre on met une orne inférieure non nulle à l'intégrale, on impose de ne recevoir que des signaux dont le décalage vers le rouge n'excède pas une certaine valeur, c'est-à-dire issues de particules dont la vitesse n'excède pas une certaine valeur. Dans ce cas, seule une portion finie de cet univers est effectivement accessible.

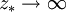
Univers en accélération (w < -1/3)

Dans le cas où le paramètre de l'équation d'état est inférieur à -1/3, l'intégrale diverge également pour une borne inférieure nulle

.

Il n'y a donc pas d'horizon cosmologique dans un tel espace, et en particulier pour l'univers de de Sitter.