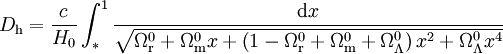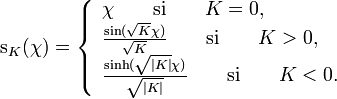Horizon cosmologique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'horizon cosmologique ou horizon cosmique est un terme d'astronomie qui désigne la limite de l'univers observable depuis un point donné (en général la Terre). Selon le contexte, il correspond soit à la limite d'où un rayonnement électromagnétique peut être issu, ou alors la limite d'où un signal de quelque nature que ce soit (neutrinos ou ondes gravitationnelles) peut être reçu. En pratique, les moyens observationnels actuels sont pour l'heure (2007) incapables de détecter des neutrinos ou ondes gravitationnelles primordiales. Plus généralement, un modèle cosmologique donné peut ou non contenir un tel horizon, c'est-à-dire des régions inaccessibles à l'observation d'un observateur donné.
L'horizon cosmologique est défini par analogie à l'horizon terrestre. De même que la courbure de la Terre limite la vision de celle-ci depuis un point fixe sur sa surface, la taille de l'univers et la vitesse de déplacement de la lumière font qu'il est impossible de voir certains objets célestes (galaxies et amas de galaxies dans ce cas) trop éloignés.
L'âge de l'univers est d'environ 13,7 milliards d'années. Par conséquent il ne nous est possible de voir que les objets dont la lumière aura voyagé pendant moins de 13,7 milliards d'années. L'univers est ainsi partagé entre une partie visible (la plus proche) et une partie invisible (la plus éloignée), la limite entre les deux zones constituant l'horizon cosmologique. Au contraire de celles de la partie visible, les galaxies situées dans la partie invisible sont trop lointaines pour que leur lumière ait eu le temps de parvenir jusqu'à nous.
Cette définition de l'horizon cosmologique ne dépend pas de l'état d'expansion de l'univers. Mais certes la position actuelle de cet horizon en dépend. Si l'univers n'était pas en expansion, la limite de visibilité d'un photon atteignant la Terre se situerait à 13,7 milliards d'années-lumière. Cependant, du fait de l'expansion de l'univers, l'objet de l'horizon cosmologique qui a émis ce photon s'est déplacé pendant la durée de voyage de la lumière et est donc situé aujourd'hui à plus de 13,7 milliards d'années-lumière. Remarquons toutefois que le photon reçu aura voyagé pendant 13,7 milliards d'années, ce qui constitue finalement une mesure utile de la distance de l'horizon cosmologique (c'est en quelque sorte une « distance temporelle »).
En pratique, les signaux les plus lointains qui nous parviennent viennent du fond diffus cosmologique. Ce rayonnement emplit tout l'univers, mais la région d'où est issu le rayonnement que nous détectons est appelé, pour des raisons évidentes, surface de dernière diffusion. Les modèles cosmologiques utilisés de nos jours, basés sur le modèle standard de la cosmologie et les équations de Friedmann, indiquent que la surface de dernière diffusion se trouverait actuellement (voir ci-dessous) à environ 46 milliards d'années-lumière de l'observateur.
C'est ce chiffre qui caractérise habituellement la distance de l'horizon cosmologique.
Calcul de la taille de l'horizon cosmologique
Il est délicat de définir des distances en cosmologie car ces distances varient au cours du temps par suite de l'expansion de l'univers (elles augmentent donc). Le concept de distance dépend beaucoup du moyen de mesure utilisé. Ainsi, les notions de distance angulaire (basée sur la taille angulaire d'un objet de taille connue) ou de distance de luminosité (basée sur le flux lumineux reçu d'un objet de luminosité connue) sont-elles différentes. Quand on parle de la taille de l'horizon, on entend distance séparant un observateur donné de l'objet le plus lointain qu'il puisse observer et rapporté à sa position actuelle, c'est-à-dire à l'époque où son temps cosmique est le même que celui de l'observateur. Les concepts de distance de luminosité ou de distance angulaires sont inadaptés pour les objets les plus distants car les objets situés à l'horizon ne sont pas détectables dans la pratique (la vision étant bornée à la surface de dernière diffusion).
La distance de l'horizon se calcule suivant une formule du type
-
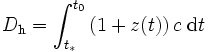
où c correspond à la vitesse de la lumière, t * et t0 correspondent respectivement à l'époque d'émission du signal le plus distant détectable et l'époque actuelle, et où la fonction z(t) donne le décalage vers le rouge d'un signal reçu aujourd'hui après avoir été émis au temps t. Une façon intuitive d'interpréter ce résultat est de dire qu'un photon parcourt la distance
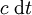
Dans le cadre d'un modèle d'univers homogène et isotrope, on peut décrire celui-ci à l'aide d'une métrique dite de Friedmann-Lemaître-Robertson-Walker. L'élément de longueur associé à cette métrique s'écrit
- ds2 = c2dt2 − a2(t)γijdxidxj,
où a(t) représente la variation temporelle des distances cosmologique (clest le facteur d'échelle) et γij correspond, au facteur a2(t) près, aux coefficients de la métrique des sections spatiales de l'univers. Celles-ci peuvent être euclidiennes, sphériques ou hyperboliques, ce que l'on peut écrire sous la forme compacte
-
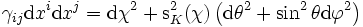
où les coordonnées des sections spatiales sont notées χ, θ et φ. Les deux dernières correspondent aux coordonnées angulaires habituelles des coordonnées sphériques usuelles, alors que χ correspond à une coordonnée radiale qui tient compte de la nature (eucilidienne ou non) des sections spatiales. La fonction s s'écrit
Le paramètre K décrit donc la nature des sections spatiales. Quand K est nul, les sections spatiales sont euclidiennes et la coordonnée χ s'identifie à la coordonnée radiale habituelle (en général notée r).
Dans cette métrique, les objets astrophysiques sont essentiellement immobiles, au sens où leurs coordonnées χ, θ, φ ne changent pas au cours du temps (omission faite de leur mouvement propre éventuel, mais celui-ci est négligeable à l'échelle cosmologique). La coordonnée t est appelée temps cosmique. Elle représente le temps mesuré par un objet immobile par rapport aux autres coordonnées. Il est commode d'effectuer un changement de variable, où le temps cosmique est remplacé par une quantité η, appelée temps conforme, selon
- cdt = a(t)dη.
Le facteur d'échelle peut alors être exprimé indifféremment en fonction de t ou de η (avec bien sûr des formes fonctionnelles différentes). L'élément de longueur se réécrit alors
-
![\mathrm{d}s^2 = a^2(\eta) \left[\mathrm{d} \eta^2 - \mathrm{d} \chi^2 - \mathrm{s}_K^2(\chi) \left(\mathrm{d}\theta^2 + \sin^2\theta\mathrm{d}\varphi^2 \right)\right]](https://static.techno-science.net/illustration/Definitions/autres/1/1c61870b8e552ba878320c32724568f6_6b1294a5637e5d83da1f47121293c251.png)
![\mathrm{d}s^2 = a^2(\eta) \left[\mathrm{d} \eta^2 - \mathrm{d} \chi^2 - \mathrm{s}_K^2(\chi) \left(\mathrm{d}\theta^2 + \sin^2\theta\mathrm{d}\varphi^2 \right)\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/1/1c61870b8e552ba878320c32724568f6_6b1294a5637e5d83da1f47121293c251.png)
La relativité restreinte enseigne que l'élément de longueur associé à la trajectoire d'un photon est nul. Si on considère la trajectoire d'un photon émis en un point dans la direction de l'originie du système de coordonnées, les coordonnées θ et φ sont en prime constantes. On a donc immédiatement
-
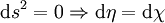
Ainsi l'intervalle en termes de temps conforme entre émission et réception du photon correspond à la variation de la coordonnée χ le long de la trajectoire. Un objet situé à la coordonné χ est distant à l'instant t0 de
- D = a(t)χ.
Pour que cet objet ait pu émettre de la lumière que nous recevons, il faut que l'intervalle en temps conforme Δη entre émission et réception du signal soit égal à χ. La distance qui nous sépare d'un objet dont on reçoit la lumière est donc
- D = a(t0)Δη.
En utilisant la formule reliant le temps conforme au temps cosmique, on trouve
-
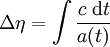
l'intégrale étant prise entre les instant d'émission du signal (noté t * ) et de réception, soit aujourd'hui (t0). On a donc
-
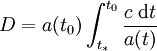
On peut en toute généralité définir le décalage vers le rouge par le rapport entre les distances entre deux galaxies lointaines à une époque donnée et aujourd'hui, selon la formule
-
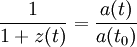
écriture qui signifie que l'on relie l'âge de l'univers t à une époque donnée au décalage vers le rouge que l'on observe aujour'hui d'un signal émis à cette époque, cette relation étant pour l'heure indéterminée. Au final, on obtient
-
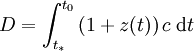
Pour calculer cette quantité, il faut connaître la relation z(t), c'est-à-dire la relation entre le décalage vers le rouge de la lumière émise par d'un objet et l'âge de l'univers à l'époque où celui-ci a émis le rayonnement reçu aujourd'hui. En d'autre terme, il faut connaître la relation entre le facteur d'échelle et le temps cosmique. Cette relation est établie par les équations de Friedmann dont c'est précisément l'objet. On trouve alors, sous certaines hypothèse, la relation suivante :
-
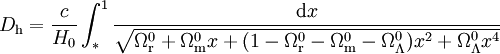
où H0 représente l'actuel taux d'expansion de l'univers (la constante de Hubble) et les différentes quantités Ω correspondent aux paramètres de densité des différentes espèces présentes dans l'univers, à savoir rayonnement et particules de masse nulle (r), matière non relativiste (matière baryonique et matière noire, m) et constante cosmologique (Λ) mesurés aujourd'hui.
Partant de l'expression
-
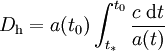
on effectue un changement de variable, où l'on remplace le temps t par la facteur d'échelle a, en utilisant la formule donnant le taux d'expansion H de l'univers,
-
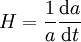
d'où
-
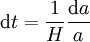
On obtient alors
-
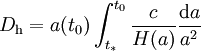
le taux d'expansion étant alors vu non pas comme une fonction du temps t, mais du facteur d'échelle a. On définit ensuite x comme le facteur d'échelle normalisé à aujourd'hui, à savoir
-
-
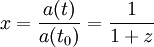
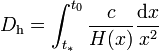
En notant H0 la valeur actuelle du taux d'expansion, on a
-
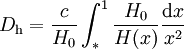
la borne d'intégration correspondant à la valeur de x à l'époque t * . Les équations de Friedmann permettent de relier le taux d'expansion aux densités d'énergie ρidu contenu matériel de l'univers selon (voir Équations de Friedmann)
-
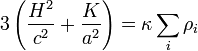
la constante κ étant la constante d'Einstein. Les densité d'énergie des espèces concernées sont des fonction du temps, et donc du facteur d'échelle. Pour une espèce dont le rapport de la pression à la densité d'énergie est wi, la densité varie en fonction du facteur d'échelle selon (voir Équation de conservation (cosmologie))
-
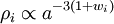
Sans perte de généralité, on peut donc écrire les densités fonction des densité d'énergie actuelles
-
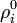
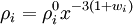
la quantité wi étant une constante ou une fonction de temps (ou de x, ce qui revient au même).
En définissant la densité critique actuelle par
-
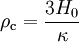
il vient, en divisant par
-
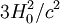
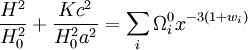
les quantité
-
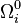
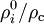
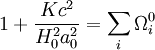
On a ainsi
-
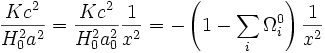
pour finalement obtenir
-
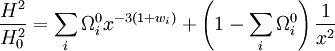
La quantité D recherchée s'exprime donc selon
-
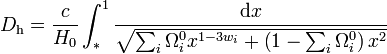
Dans le cas où le contenu matériel de l'univers se réduit à de la radiation (pression égale à un tiers de la densité d'énergie, wr = 1 / 3), de la matière non relativiste (pression négligeable, wm = 0) et une constante cosmologique (pression opposée à la densité d'énergie, w = − 1), alors on retrouve bien
-
