Lexique de la théorie des graphes - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
R
- Rayon : excentricité minimale des sommets, notée R.
- Régulier : un graphe est k-régulier si chacun de ses sommets est de degré k.
- Relation de Djokovìc-Winkler : deux arêtes exy et euv sont en relation de Djokovìc-Winkler, et on le note exyΘeuv si on a l'inégalité
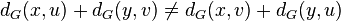
T
- Technique spectrale : technique faisant intervenir le spectre du graphe.
- Transversal : un transversal (ou couverture nodale, ou support) d'un graphe est un sous-ensemble de sommet T tel que toute arête du graphe est incidente à au-moins un sommet de T. Le complémentaire d'un transversal est un stable.
- Triangle : cycle de longueur trois.
- Triangulé : un graphe est triangulé s'il ne contient pas un cycle de longueur quatre sans corde comme mineur. Les arbres, et les graphes d'intervalles notamment, sont triangulés.
- Trivial : un graphe est trivial s'il a un seul (graphe singleton) ou aucun sommet (graphe nul). On peut utiliser un graphe trivial pour commencer une preuve par récurrence, mais ils sont implicitement exclus des théorèmes dont ils constitueraient parfois des contre-exemples inintéressants.
| Sommaire : | - |
|---|
V
- Valuation : fonction associant un poids à chaque arête.
- Vecteur d'intersection : séquence {b0,b1,...bD,c1,c2,...,cD} d'un graphe distance-régulier.
Z
- Références pour la terminologie non-standard
- (en) Irène Charon, Iiro Honkala, Olivier Hudry et Antoine Lobstein - Structural properties of twin-free graphs, The electronic journal of combinatorics, volume 14, 2007.
- (en) D. Djokovìc - Distance preserving subgraphs of hypercubes, Journal of Combin. Theory. Ser. B, numéro 14, pages 263-267, 1973.
- (en)Dragos M. Cvetkovic et Michael Doob et Horst Sachs - Spectra of Graphs, Heidelberg, Leipzig, 1994, .

















































