Lexique de la théorie des graphes - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Introduction
| Sommaire : | - |
|---|
A
- Acyclique (graphe) : graphe ne contenant pas de cycle.
- Adjacence (liste d') : structure de données constituée d'un tableau dont le ie élément correspond à la liste des voisins du ie sommet.
- Adjacence (matrice d') : matrice d'éléments aij correspondant au nombre d'arêtes ayant pour extrémités les sommets d'indices i et j.
- Adjacence (relation d') : propriété de deux sommets d'être connectés par la même arête (on parle de sommets adjacents) ou propriété de deux arêtes de présenter une extrémité commune (on parle d’arêtes adjacentes). Synonyme : relation de voisinage.
- Adjoint (graphe) : synonyme de line graph.
- Admittance : autre nom d'une matrice laplacienne.
- Aléatoire (graphe) : un graphe est aléatoire, ou non déterministe, dès que sa construction fait intervenir des probabilités.
- Arbre : graphe connexe sans cycle. Équivalent à : graphe connexe à n sommets et n − 1 arêtes.
- Arbre enraciné ou arborescence : graphe acyclique orienté où on distingue une racine de degré entrant nul, et où tous les autres sommets sont de degré entrant 1.
- Arc : arête dans un graphe orienté. Autre formulation : couple (ensemble ordonné de deux éléments) de sommets reliés par une arête dans un graphe non orienté.
- Arc-transitif (graphe) : on dit qu'un graphe G est arc-transitif si son groupe d'automorphisme agit transitivement sur l'ensemble de ses arcs. Étant donné deux arêtes
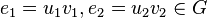
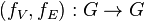
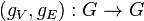
- Arête : connexion entre deux sommets A et B. Dans le cas des graphes orientés on parle d'arc. Le terme « arête » est alors utilisé pour désigner l'ensemble des deux arcs (A,B), c'est-à-dire de A vers B, et (B,A), c'est-à-dire de B vers A.
- Arête multiple : ensemble d'arêtes parallèles relatif à un couple de sommets.
- Arête parallèle : arête ayant pour extrémités les mêmes sommets qu'une autre arête. On parle d'arêtes parallèles.
- Arête-transitif (graphe) : on dit qu'un graphe est arête-transitif si son groupe d'automorphisme agit transitivement sur l'ensemble de ses arêtes. Autre formulation de la condition : pour tout couple d'arêtes, au moins un automorphisme envoie la première composante sur la seconde. Toutes les arêtes jouent exactement le même rôle à l'intérieur du graphe. Exemple : un graphe complet.
- Automorphisme : isomorphisme d'un graphe sur lui-même. Chaque graphe possède au moins un automorphisme : l'identité. L'ensemble des automorphismes d'un graphe forme un groupe.
C
- Chemin : soit un graphe G = (V,E). Un chemin P = (S,A) est défini par S = {s0,...,sk}, A = {s0s1,...,sk − 1sk},
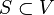
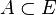
- Circonférence : longueur du plus grand cycle.
- Clique : sous-graphe induit complet, c'est-à-dire un sous-ensemble des sommets tels que chacun est connecté à tous les autres. Une clique est un ensemble indépendant (ou stable) du graphe complémentaire.
- Coloration : fonction associant à tout sommet une couleur, tels que deux sommets adjacents aient une couleur différente (c'est-à-dire partitionne les sommets en ensembles indépendants). Le nombre minimum de couleurs pour un graphe G est le nombre chromatique dénoté χ(G).
- k-coloration : coloration d'un graphe en k couleurs distinctes.
- Complémentaire : le complémentaire (ou inverse, ou complément)
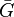
![\bar{G} = (V, [V]^2 \backslash E)](https://static.techno-science.net/illustration/Definitions/autres/9/965a8d2506e2cd52e31d5dbd5eccbafb_5ba18141ff53d4a94d603d6b2c88400f.png)
- Complet : dans un graphe complet chaque sommet est relié à tous les autres. On note Kn le graphe complet à n sommets.
- Composante : un composante d'un graphe est un sous-graphe connexe maximal.
- Connexe : un graphe est connexe s'il existe un chemin entre tout couple de sommets. Quand on parle de connexité pour un graphe orienté, on considère non pas ce graphe mais le graphe non-orienté correspondant. On peut déterminer ceci par exemple avec un algorithme de parcours en profondeur. Un graphe orienté est dit fortement connexe si, pour tout couple de sommets (u,v) du graphe, il existe un chemin de u à v et de v à u.
- k-arête-connexe : un graphe est k-arête-connexe s'il cesse d'être connexe uniquement quand on supprime k arêtes; ceci peut se vérifier par la présence de k chaînes disjointes (ne partageant aucune arête) entre chaque sommet.
- k-sommet-connexe (ou k-connexe) : un graphe est k-sommet-connexe s'il cesse d'être connexe uniquement quand on supprime k sommets.
- Contenir : on dit d'un graphe G qu'il contient H si H est un sous-graphe induit de G.
- Contraction : supprime une arête d'un graphe en fusionnant ses deux extrémités. Autrement dit, la contraction G / e d'une arête exy à un sommet x rend le sommet x adjacent à tous les voisins précédents de y.
- Corde : arête reliant deux sommets non-adjacents d'un cycle
- Cospectral : deux graphes sont cospectraux s'ils ont le même spectre. Ce spectre pouvant être basé sur plusieurs matrices, on peut préciser A-cospectraux pour le spectre de la matrice d'adjacence et L-cospectraux pour le spectre de la matrice laplacienne.
- Cubique : graphe 3-régulier.
- Cycle : chemin dont les sommets de départ et de fin sont les mêmes. Autrement dit, soit un chemin dont les arêtes sont E = {s0s1,...,sk − 2sk − 1} : le cycle est alors défini par
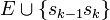
- Cyclomatique : le nombre cyclomatique d'un graphe G = (V,E) est M = | E | − | V | + P, où P est le nombre de composantes connexes. C'est également la dimension de l'espace des cycles.
| Sommaire : | - |
|---|

















































