Lexique de la théorie des graphes - Définition

O

• Ordre : nombre de sommets du graphe.
• Orienté : un graphe est orienté si les arêtes ont un sens, par exemple e_uv indique qu'il y a un arc de u à v. Un graphe est non-orienté si ses arêtes n'ont pas de sens  : e_uv indique qu'il y a une arête entre u et v.
• Outer-planar : dans un graphe planaire, on considère les régions (ou faces) entourées par des arêtes comme internes. L'ensemble du graphe est donc entouré par une région externe. Si toutes les faces internes sont adjacentes à la face externe, alors le graphe est outer-planar.

N

• Noeud : terminologie utilisée dans les réseaux pour un sommet. Un noeud interne est un sommet dans un arbre de degré supérieure à 1, c'est-à-dire n'étant pas une feuille.
• Noyau : sous-ensemble de sommets à la fois stable et dominant.

P

• Parfait : un graphe est parfait si le nombre chromatique de chacun de ses sous-graphes induits H est égal à la taille de la clique maximale de H.
• Partition : séparation des sommets du graphe en des ensembles disjoints de sommets dont l'union permet de retrouver tous les sommets. Formellement, une partition sépare V en tel que et .
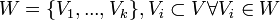
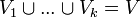
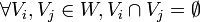
• Petit monde : un graphe a le phénomène du petit-monde si son coefficient de clustering est élevé et la distance moyenne entre deux sommets faible. Cette notion provient de la physique, et il n'y a pas de définition exacte quant à ce qui est élevé et ce qui est faible; on considère la distance moyenne comme faible tant qu'elle n'excède pas le logarithme du nombre de sommets.
• Planaire : un graphe est planaire si on peut le dessiner dans un plan sans croiser deux arêtes. Un graphe est planaire s'il ne contient pas K₅ et K_3,3 comme mineurs.
• Plongement : soient deux graphes G₁ = (V₁,E₁),G₂ = (V₂,E₂). Un plongement est une fonction injective de V₂ dans V₁ tel que chaque arête de V₂ corresponde à un chemin disjoint de G₁. Un plongement permet de dire qu'on peut utiliser un graphe pour simuler les capacités de l'autre en termes de connexion : s'il y a une arête (i.e. un chemin dédié) entre deux sommets, alors on la retrouvera dans le graphe simulant sous la forme d'un chemin dédié (mais pouvant être plus long).
• Polynôme caractéristique : le polynôme | λI − A | de la matrice d'adjacence A d'un graphe G est son polynôme caractéristique, et on le note P_G(λ).
• Pondéré : un graphe pondéré est celui auquel on adjoint une fonction de valuation.
• Pont : dans un graphe connexe, un pont est une arête dont la suppression déconnecte le graphe.
• Promenade (ou parcours) : voir chemin (considéré en général comme non-élémentaire). Une promenade close (ou parcours fermé) est un cycle.
• Puits : dans un problème de flot, sommet consommant le flot. Généralement de degré sortant nul, mais pas nécessairement.

S

• Simple (ou Schlicht) : graphe fini, non orienté, sans boucles ni arêtes multiples.
• Sommet-transitif : on dit qu'un graphe est sommet-transitif si son groupe d'automorphisme agit transitivement sur l'ensemble de ses sommets. Autre formulation de la condition : pour tout couple de sommets, au moins un automorphisme envoie la première composante sur la seconde. Tous les sommets jouent exactement le même rôle à l'intérieur du graphe. Un graphe sommet-transitif est ainsi nécessairement régulier.
• Source (dans un problème de flot) : sommet produisant le flot. Un tel sommet est généralement de degré entrant nul, mais pas nécessairement.
• Sous-graphe : graphe contenu dans un autre graphe. Formellement, avec des notations intuitives, un graphe H = (V_H,E_H) est un sous-graphe de G = (V_G,E_G) si et .
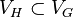
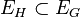
  H est un sous-graphe couvrant ou graphe partiel de G (i.e. H couvre G) si, en plus, tous les sommets de G sont dans H (V_H = V_G).
  H est un sous-graphe induit de G si, pour tout couple (x,y) de sommets de H, x est connecté à y dans H si et seulement si x est connecté à y dans G. Autre formulation de la condition : l'ensemble des arêtes de H correspond à l'ensemble des arêtes de G incidentes à deux sommets de H.
• Spanner : sous-graphe couvrant dont on essaye de minimiser le nombre d'arêtes (i.e. la densité) tout en conservant des bonnes propriétés de distance. Dans un spanner additif (respectivement multiplicatif), la distance entre deux sommets peut être augmentée (respectivement multipliée) jusqu'à un certain facteur appelé le délai (respectivement la dilatation).
• Spectre : ensemble des valeurs propres d'une matrice représentant le graphe. La matrice peut être de Laplace ou d'adjacence. Les relations entre le spectre du graphe et ses propriétés font l'objet de la théorie spectrale des graphes.
• Stable (ensemble) : ensemble de sommets 2 à 2 indépendants. Synonyme : ensemble indépendant.
• Subdivision : la subdivision d'un graphe consiste à ajouter des sommets sur les arêtes, c'est-à-dire à remplacer des arêtes par des chemins. En particulier S(G) est le graphe où chaque arête de G a été remplacée par un chemin de longueur deux par insertion d'un sommet dans chaque arête.
• Symétrique : un graphe est symétrique s'il est à la fois arête-transitif et sommet-transitif. Cela revient à vérifier que toutes ses arêtes et tous ses sommets sont indistinguables en termes d'isomorphisme de graphe. Exemple : graphe de Petersen.