Maîtrise statistique des procédés - Définition
La liste des auteurs de cet article est disponible ici.
Normalité d'une distribution
Généralités
Les tests qui suivent permettent de s'assurer de la normalité des résultats obtenus.
Droite de Henry
Sur un simple examen de l'histogramme, il n'est pas évident de se prononcer sur la 'normalité' des variables. Il est pratique de comparer le graphique obtenu avec les données théoriques correspondantes basées sur une loi théorique standardisée et de représenter ces données sur une droite à l'aide d'un changement d'échelle. La droite de Henry permet de réaliser cette transformation. On constate que la distribution de l'exemple 1 est quasi-normale.
La droite de Henry coupe l'axe des x au point d'abscisse m et sa pente est égale à 1/σ, ce qui permet une estimation de l'écart-type de la distribution.
Moyenne de moyennes de données
Si l'on suppose que la population dont on a extrait l'échantillon est normale et a pour paramètres théoriques X = 133 mm (moyenne) et σ = 5 mm, alors on peut tracer l'histogramme de loi normale centrée réduite correspondante sur une simulation de 1000 pièces tirées au hasard. La moyenne théorique est de 133 mm, l'écart type de 5 mm et l'étendue de 34 mm. Puisque notre échantillon de 32 données suit approximativement une loi normale, on peut se poser la question de savoir si la moyenne théorique de la population serait plus précise si on multipliait le nombre des séries d'observations. Simulons par exemple 9 prélévements successifs de 1000 pièces de moyenne théorique 133 mm et d'écart type 5 mm. La moyenne théorique obtenue est de 120mm, l'écart type de 4,8 mm et l'étendue de 32 mm. La distribution de la 'moyenne des moyennes' semble normale. L'histogramme est centré sur la moyenne théorique (120), mais la distribution de la moyenne est plus ressérée que dans l'histogramme ci-dessus. La moyenne de l'échantillon donne donc une moyenne plus précise de la moyenne théorique qu'une seule série d'observations X. Soit Mm, la moyenne des moyennes.
On démontre que pour n séries d'observations :
- Moyenne Mm = moyenne (X )d'une série d'observations.
- Écart type de Mm =
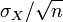
- Variance de Mm = variance (X) / n.
Théorème de la limite centrale
En contrôle qualité, la plupart des distributions de données d'échantillons suivent une loi normale. Si toutefois les données ne semblent pas « normales », le théorème de la limite centrale permet d'affirmer que la moyenne d'une variable indépendante distribuée de façon quelconque devient une variable normale quand le nombre d'observations est assez grand.
La moyenne arithmétique
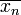
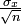
Donc, si n est > 5, par exemple, la distribution des moyennes
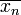
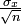
Test du khi-deux
Cartes de contrôle
La carte de contrôle est le principal outil de la MSP. On se propose de tracer les cartes de contrôle à la moyenne et à l'étendue de l'exemple.
| N° | X1 | X2 | X3 | X4 | X5 | X | R |
|---|---|---|---|---|---|---|---|
| 1 | 130 | 136 | 135 | 137 | 138 | 135,2 | 5,2 |
| 2 | 134 | 133 | 135 | 135 | 137 | 134,8 | 5,2 |
| 3 | 137 | 136 | 135 | 135 | 133 | 135,2 | 5,2 |
| 4 | 135 | 135 | 138 | 137 | 137 | 136,4 | 5,2 |
| 5 | 135 | 134 | 135 | 138 | 137 | 136,4 | 5,2 |
| 6 | 135 | 134 | 135 | 135 | 138 | 135,4 | 5 |
| 7 | 138 | 135 | 138 | 135 | 138 | 136,4 | 4,9 |
| 8 | 134 | 140 | 135 | 132 | 135 | 135,2 | 4,9 |
| 9 | 135 | 133 | 133 | 135 | 135 | 134,2 | 4,9 |
| 10 | 134 | 134 | 135 | 138 | 137 | 135,6 | 5,1 |
| 11 | 132 | 139 | 135 | 138 | 135 | 135,8 | 5 |
| 12 | 134 | 140 | 135 | 135 | 137 | 136,2 | 5,1 |
| 13 | 131 | 139 | 130 | 135 | 135 | 134 | 5 |
| 14 | 134 | 135 | 139 | 138 | 135 | 136,2 | 4,9 |
| 15 | 136 | 135 | 139 | 131 | 135 | 135,2 | 4,9 |
| 16 | 133 | 133 | 135 | 132 | 131 | 132,8 | 5,1 |
| 17 | 135 | 131 | 131 | 135 | 135 | 133,4 | 4,9 |
| 18 | 135 | 135 | 138 | 131 | 131 | 134 | 5,3 |
| 19 | 131 | 139 | 133 | 135 | 132 | 134 | 4,9 |
| 20 | 131 | 138 | 136 | 135 | 138 | 135,6 | 5,1 |
Pièce : clé métallique.
Caractéristique : Longueur.
Unité de mesure : mm.
Fréquence de contrôle : toutes les 2 heures.
En appliquant les coefficients de calcul des limites pour 5 prélèvements par échantillon, on calcule pour chaque ligne, la moyenne X et l'étendue R par échantillon, puis la moyenne des moyennes et l'étendue moyenne sur l'ensemble des échantillons. (20 lignes)
A2 = 0,577
D4 = 2,115
D3 = 0
Pour la carte à la moyenne (en haut), les limites du contrôle sont :
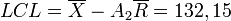

Pour la carte à l'étendue (en bas) :
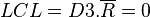
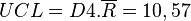
Le procédé de fabrication est sous contrôle.

















































