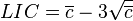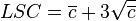Carte de contrôle - Définition
Une carte de contrôle est un outil permettant de determiner le moment où apparaît la cause assignable entraînant la dérive. Ainsi, le processus sera arrêté au bon moment, c’est-à-dire avant qu'il ne produise des pièces non conformes (hors de l'intervalle de Tolérance).
Les cartes de contrôle les plus utilisées sont les cartes de contrôle par mesure de la moyenne et de l'étendue. Ces cartes sont établies ensemble et interprétées ensemble. En effet, la distribution des dimensions fabriquées modélisée par une loi Normale est caractérisée par la moyenne et la dispersion (écart type).
SPC et contrôle qualité
Le créateur de la carte de contrôle est Walter A. Shewhart qui travailla au Bell Telephone Laboratory de la Western Electric. Shewart publia en 1931 les principes de la variabilité d'un procédé en distinguant la variabilité aléatoire naturelle et la variabilité accidentelle. la variabilité naturelle est issue de 'causes communes de dispersion' ou 'perturbations normales' intégrées dans le processus de fabrication 'sous contrôle'. La variabilité accidentelle est dûe à des 'causes spéciales' occasionnelles et incontrôlées (matières premières aux caractéristiques fluctuantes, machines mal réglées, horaires de travail différents, qualification de la main-d'oeuvre, changements de température ou de pression, mauvaise lubrification ...). La SPC a pour mission de déterminer si le processus est sous contrôle ou non. Une analyse plus détaillée des causes des variations permettra d'améliorer ses performances et sa régularité. Les cartes de contrôle sont un outil graphique de visualisation du processus de fabrication dans le temps et de mise en évidence de sa stabilité (surveillance des causes spéciales).
La carte de contrôle
Elles permettent d'effectuer un réglage opportun du procédé de fabrication et de connaître sa capabilité machine. Cet outil se présente comme un graphique dont les points représentent le suivi dans le temps d'une caractéristique du processus dont la valeur centrale (souvent la moyenne) est représentée par une ligne horizontale ainsi que les limites inférieure (LCL) et supérieure (UCL) (UCL : Upper Control Limit, LCL : Lower Control Limit).
Ces deux valeurs sont les limites à l'intérieur desquelles le processus est sous contrôle. Les valeurs de la caractéristique contrôlée doivent se trouver à l'intérieur des ces limites, sinon ces valeurs sont 'hors contrôle' et doivent être examinées.
Différentes cartes de contrôle
Deux cartes de contrôle sont nécessaires pour surveiller la position et la dispersion.
Cartes pour variables quantitatives
Les variables quantitatives sont des mesures continues (poids, longueur, épaisseur, température, diamètre..). On vérifie sur la carte de contrôle de la moyenne (mean chart) ou sur la carte d'étendue (range chart) que le caractère étudié sera stable dans le temps. La taille de l'échantillon est de 4 à 6.
Cartes pour variables qualitatives
Pour mesurer des variables qualitatives (% de défectueux, ¨% de pannes...), on se sert de cartes aux attributs p, np ou c pour contrôler les attributs dans le temps. La taille d'échantillon est de l'ordre de 50 à 100.
Carte de contrôle à la moyenne et de l'étendue
Ces deux paramètres sont indépendants et complémentaires. La valeur moyenne peut varier sans que la dispersion ne varie et inversement.
Ces cartes de contrôle permettent de visualiser l'évolution de la dispersion des dimensions fabriquées. La carte de contrôle de l'écart type est "plus juste" et moins dispersée que la carte de contrôle de l'étendue. Par contre, les calculs a réaliser pour tracer la carte de contrôle de l'entendue sont moins compliqués et donc plus fiables. La carte de contrôle de l'écart type sera mise en oeuvre si le tracé de la carte est informatisé ou assisté par un outil de calcul automatique. La carte de contrôle de l'étendue sera en oeuvre si le tracé de la carte de contrôle est manuel sur un support papier.
But
Cette carte de contrôle permet de visualiser l'évolution et la variation de la valeur moyenne des dimensions fabriquées. Cette carte de contrôle est tracée par points successifs représentant la valeur moyenne d'échantillon prélevés à intervalles réguliers.
Le but est de comparer les performances moyennes de production dans le temps à l'aide d'une carte qui caractérise la tendance de la valeur centrale. On effectue plusieurs observations individuelles sur plusieurs sous-groupes numérotés à une fréquence de temps donnée (toutes les heures, trois fois par jour ...). Sur chaque sous-groupe k chronologique on effectue n observations. On reporte sur la carte de moyenne la moyenne du sous-groupe en fonction de son numéro chronologique qui sera reporté sur l'axe horizontal des cartes de contrôle. En raison du théorème limite central, la moyenne des valeurs sur la carte de contrôle suit une loi normale que les observations soient normalement distribuées ou non.
Cette loi est valable même pour des échantillons de petite taille, ce qui est fréquent en contrôle qualité. Une production sera dite 'stable',si la tendance et la dispersion sont statistiquement constantes dans le temps. La carte de contrôle à la moyenne surveille le réglage du procédé, la carte des étendues les dispersions.
Limites du contrôle
L'écart type est connu
Le calcul des limites de la carte de moyenne diffère selon que l'écart-type est connu ou non.
Lorsque l'écart-type du processus est connu, les caractéristiques de la distribution normale permettent de calculer les limites du contrôle. L'intervalle [μ − 3σ; − μ + 3σ], contient 99.7 % des données et représente les limites LCL et UCL des cartes de contrôle. La probabilité pour qu'un point se trouve à l'extérieur des limites est donc 0,3%. La valeur de la moyenne diffère sensiblement selon que l'écart type de la population est connu ou non. Si la vraie valeur de la moyenne µ des observations est inconnue, on peut la remplacer par la moyenne par échantillon
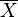
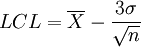
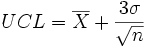
94,74% des points doivent se trouver entre les limites si le processus est sous contrôle. L'interprétation de la carte de la moyenne est la même si la vraie moyenne du processus est connue ou inconnue.
L'écart type est inconnu
Dans beaucoup de cas, l'écart type σ est inconnu et doit être estimé par t (loi de Student) au lieu de la loi normale standard. On se sert alors d'un coefficient A2 qui dépend du nombre d'observations dans chaque échantillon et du type de carte utilisé. Les limites de contrôle sont estimées en utilisant l'étendue moyenne des observations à l'intérieur d'un sous-groupe comme mesure de variabilité.
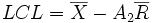
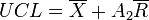
avec:
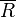
Elle est égale à la moyenne des étendues (valeur maximale du sous-groupe - valeur minimale) de chaque sous-groupe.Les limites se resserrent quand la taille du sous-groupe des échantillons augmente.
un exemple
La société Emballex fabrique des boîtes métalliques dont on contrôle le poids à la sortie de fabrication. Cette caractéristique dépend essentiellement de la composition des matières premières et de la qualité de l'alliage réalisé. L'entreprise décide de contrôler le procédé de fabrication à l'aide de cartes de contrôle pour le poids moyen des pièces et l'étendue du poids pour chaque échantillonnage effectué. Le contrôle consiste à prélever 5 boîtes à la sortie de la machine et de peser chaque boîte. le poids exprimé en grammes. Les poids ont été enregistrés sur une série de 20 échantillons prélevés.
Tracer les cartes de contrôle pour les cartes X et R.
| N° éch | X1 | X2 | X3 | X4 | X5 | Moy | Ete |
|---|---|---|---|---|---|---|---|
| 1 | 81 | 85 | 82 | 84 | 83 | 83 | 4 |
| 2 | 86 | 81 | 83 | 84 | 80 | 82 | 6 |
| 3 | 87 | 87 | 87 | 88 | 82 | 86,2 | 5 |
| 4 | 87 | 85 | 89 | 86 | 84 | 85,2 | 6 |
| 5 | 81 | 89 | 86 | 85 | 87 | 85,6 | 8 |
| 6 | 84 | 81 | 87 | 87 | 84 | 84,6 | 6 |
| 7 | 84 | 87 | 93 | 87 | 85 | 87,2 | 9 |
| 8 | 87 | 86 | 82 | 87 | 86 | 85,6 | 5 |
| 9 | 83 | 79 | 87 | 84 | 86 | 83,8 | 8 |
| 10 | 85 | 82 | 85 | 84 | 86 | 84,4 | 4 |
| 11 | 81 | 83 | 85 | 85 | 84 | 83,6 | 4 |
| 12 | 85 | 79 | 78 | 83 | 86 | 82,2 | 8 |
| 13 | 87 | 83 | 89 | 85 | 80 | 84,8 | 9 |
| 14 | 87 | 86 | 86 | 79 | 83 | 84,2 | 8 |
| 15 | 89 | 82 | 86 | 86 | 85 | 85,6 | 7 |
| 16 | 90 | 84 | 81 | 85 | 83 | 84,6 | 9 |
| 17 | 86 | 82 | 85 | 86 | 88 | 85,4 | 6 |
| 18 | 85 | 83 | 83 | 85 | 89 | 85 | 6 |
| 19 | 80 | 81 | 83 | 87 | 82 | 82,6 | 7 |
| 20 | 85 | 89 | 82 | 79 | 83 | 85,6 | 10 |
Le poids moyen est 84,5 g.
La limite supérieure est 87,81 g.
La limite inférieure est 81,18 g.
Le procédé de fabrication est sous contrôle.
Carte à l'étendue
Cartes de contrôle de l'étendue : Cette carte de contrôle permet de visualiser l'évolution et de la variation de l'étendue (image de la dispersion) des dimensions fabriquées. Cette carte de contrôle est tracée par points successifs représentant l'étendue d'échantillons prélevés à intervalles reguliers.
Les limites de contrôle sont les suivantes :
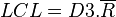
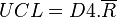
avec:
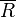
Ri étendue du sous-groupe i. k: nombre de sous-groupes. La moyenne des étendues indique l'importance de la variabilité naturelle du procédé. Pour l'exemple ci-dessus, l'étendue moyenne est 6,750 g.
La limite inférieure est: 0 g.
La limite supérieure est: 14,28 g.
Le procédé de fabrication est sous contrôle.
Coefficients
Ces coefficients servent à calculer les limites de contrôle en fonction de la taille des échantillons et du type de carte utilisée.
| Taille | A2 | D3 | D4 | Sigma |
|---|---|---|---|---|
| 2 | 1,880 | 0 | 3,267 | 1,128 |
| 3 | 1,023 | 0 | 2,575 | 1,693 |
| 4 | 0,729 | 0 | 2,282 | 2,059 |
| 5 | 0,577 | 0 | 2,115 | 2,326 |
| 6 | 0,483 | 0 | 2,004 | 2,534 |
| 7 | 0,419 | 0,076 | 1,924 | 2,707 |
| 8 | 0,373 | 0,136 | 1,864 | 2,847 |
| 9 | 0,337 | 0,184 | 1,816 | 2,970 |
| 10 | 0,308 | 0,223 | 1,777 | 3,078 |
| 11 | 0,285 | 0,256 | 1,744 | 3,173 |
| 12 | 0,266 | 0,284 | 1,716 | 3,258 |
| 13 | 0,249 | 0,308 | 1,692 | 3,336 |
| 14 | 0,235 | 0,329 | 1,671 | 3,407 |
| 15 | 0,223 | 0,348 | 1,652 | 3,472 |
| 16 | 0,212 | 0,364 | 1,636 | 3,532 |
| 17 | 0,203 | 0,379 | 1,621 | 3,588 |
| 18 | 0,194 | 0,392 | 1,608 | 3,640 |
| 19 | 0,187 | 0,404 | 1,596 | 3,689 |
| 20 | 0,180 | 0,414 | 1,586 | 3,735 |
Cartes de contrôle aux attributs
Si l'on ne désire pas effectuer un contrôle de variables par mesures, ou si cela n'est pas possible, on préfèrera la contrôle de la qualité par attributs qui consiste à noter la présence ou l'absence d'un critère qualitatif sur les pièces contrôlées. Exemples: contrôle visuel (absence de défaut ou non), dimension trop petite ou trop grande (passage de la pièce dans un calibre)....
Les principales cartes de contrôle aux attributs sont:
1- La carte p pour la proportion de défectueux.
2- La carte np pour le suivi du nombre de défectueux.
3- La carte c pour le suivi du nombre de défauts.
Carte p
Principe
On utilise cette carte pour suivre la proportion p de défectueux contenus dans un échantillon en provenance d'un lot ou d'une machine. Sur un prélèvement au hasard, à intervalle régulier, d'un échantillon de n pièces, on note le nombre de défectueux trouvés que l'on divise par l'effectif de l'échantillon n (n > 50) pour obtenir p.
p = nombre de pièces défectueuses / nombre de pièces dans l'échantillon = d / n
On reporte périodiquement p sur une carte de contrôle où l'on fera apparaître la moyenne de proportion des défectueux et les limites inférieures et supérieures correspondantes.
La proportion moyenne de défectueux sur l'ensemble des prélèvements est:
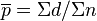
Les limites de contrôle se situent à 3 écarts-types de chaque côté de la proportion moyenne.
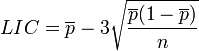
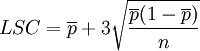
La loi qui régit la carte de contrôle p est la loi binomiale: constatation de d pièces défectueuses (deux modalités) sur un prélèvement au hasard de n pièces. Lorsque n est grand, une approximation par la loi normale est légitime. L'intervalle [μ − 3σ; − μ + 3σ], contient alors 99.7 % des données contenues dans les limites LCL et UCL des cartes de contrôle.
Exemple
L'entreprise GLASSEX fabrique des poignées en matière plastique utilisées dans l'ameublement des cuisines et salles de bain. On effectue un contrôle visuel toutes les heures sur un échantillon de 65 poignées pour détecter les principaux défauts: éraflures, couleur douteuse, microfissures, etc...afin de suivre le taux de défectueux dans le procédé de fabrication. Les résultats sur 28 séries d'échantillons sont mentionnés dans le tableau ci-contre.
On obtient une moyenne pour p de 0,079 avec un écart type moyen de 0,031 de défectueux.
La limite supérieure de la carte p est 0.179.
Carte np
L'utilisation de la carte np est recommandé si l'effectif n de l'échantillon demeure le même pour chaque série d'échantillons. On reporte sur la carte np le nombre de défectueux observés chronologiquement dans les prélèvements successifs. Le nombre de défectueux dans un échantillon de taille n est d = np. Pour k prélèvements d'effectif n, le nombre moyen de défectueux est:
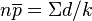
avec
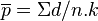
On peut calculer les limites de contrôle basées sur des intervalles de trois écarts-types autour du nombre moyen de défectueux.
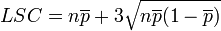
Carte c
La carte c est utilisée pour suivre chronologiquement le nombre de défauts par unité contrôlée (100 mètres de câble, 20 mètres de rouleau de papier peint,...). Elle est différente des cartes p et np, car le critère suivi est le nombre de défauts et non le nombre de défectueux (refusés), une pièce présentant des défauts pouvant être ou non acceptée. Suivant le critère de gravité du défaut (critique, majeur ou mineur), la pièce sera ou non considérée comme défectueuse. Le nombre moyen de défauts observés sur k unités contrôlées est :
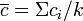
ci est le nombre de défauts observé pour la i ième unité contrôlée. Les limites de contrôle sont donc: