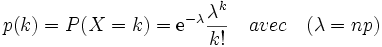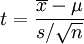Maîtrise statistique des procédés - Définition
La liste des auteurs de cet article est disponible ici.
Notions de statistiques appliquées au contrôle qualité
Les méthodes et outils MSP font appel aux statistiques et plus précisément à la statistique mathématique.
Distribution de variables aléatoires discrètes
Généralités
Une population est un ensemble d'individus (pièce mécanique, échantillon de sable, boîtes..) sur lequel on suivra un ou plusieurs caractères (couleur, température, dimension, concentration, pH, etc.). Ce caractère peut être qualitatif (aspect, bon ou défectueux) ou quantitatif (taille, poids, nombre de défauts). Dans ce dernier cas, les valeurs prises par le caractère constitueront une distribution discontinue ou continue. En pratique, les observations seront effectuées sur une partie de la population (échantillon statistique) prélevée au hasard.
Distribution binomiale
La loi binomiale est utilisée lors d'un tirage non exhaustif (avec remise). Elle peut être utilisée lorsque le rapport de la taille de l'échantillon (n) sur celle du lot (N) est telle que n / N
La probabilité pour qu'il y ait k pièces défectueuses dans n tirages non exhaustifs (indépendants) est :
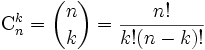
Exemple : Il s'agit d'évaluer les probabilités (P) d'observer X = 0,1,2,3,4,5 pièces défectueuses dans un échantillon de taille n =5 avec p =0,10 et q =0,90. La pièce est classée défectueuse si le diamètre est trop petit ou trop grand. La machine outil fournit 10% de pièces défectueuses dans un échantillon de taille 5.
| X | P |
|---|---|
| 0 | 0,59049 |
| 1 | 0,32805 |
| 3 | 0,0729 |
| 4 | 0,00045 |
| 5 | 0 |
Cette loi est utilisée très souvent dans le contrôle de réception par attributs ou lors du contrôle de réception d'un lot. La variable binomiale suit une distribution discrête ne pouvant prendre que les valeurs entières 0,1,2,...,n.
Distribution hypergéométrique
Lorsqu'un contrôle implique la destruction complète des pièces ou éléments à contrôler, il est impossible d'effectuer un tirage exhaustif (sans remise). La loi hypergéométrique est utilisée à la place de la loi binomiale et sa représentation graphique est proche de cette dernière. La loi hypergéométrique a pour expression :
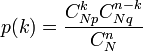
(q = 1 -p)
N: taille du lot.
n: taille de l'échantillon (n < N).
p: % de défectueux dans le lot initial.
C: nombre total de défectueux dans le lot.k : nombre de produits défectueux possibles dans l'échantillon de taille n.
Distribution de Poisson
Lorsque n est grand et p faible, la loi de Poisson constitue une approximation de la loi binomiale. La probabilité d'avoir k pièces défectueuses dans un échantillon n donné est :
Une application courante de la loi de Poisson est la prédiction du nombre d'événements susceptibles de se produire sur une période de temps déterminée, par exemple, le nombre de voitures qui se présentent à un poste de péage en l'espace d'une minute. La loi de Poisson est une approximation de la loi binomiale si n > 40 et p < 0,1.
Distributions de variables aléatoires continues
Distribution normale
L'analyse des variables intervenant dans la production d'une machine (diamètre des pièces produites, poids ...) montre que si le réglage est constant, la répartition suit une courbe 'en cloche' dont les deux caractéristiques importantes sont la moyenne et la dispersion. La loi normale est très utilisée en contrôle statistique, surtout sous sa forme centrée réduite. wikisource: Table de la fonction de répartition de la loi normale centrée réduite. Dans la pratique MSP, une notion comme l'intervalle de confiance, est basée sur les probabilités de la loi normale. Par exemple, 68,3% de la surface sous la courbe d'une distribution normale signifie que 2/3 des observations se trouveront dans l'intervalle : [μ − σ; − μ + σ]. De même on estime à 95,4% la probabilité pour qu'une observation (dispersion = 6 fois l'écart type) se trouve dans l'intervalle: [μ − 2σ; − μ + 2σ]. L'intervalle [μ − 3σ; − μ + 3σ], contient 99.7 % des données. La loi normale est définie par ses deux premiers moments (m et σ). Son coefficient d'asymétrie est nul et son coefficient d'aplatissement égal à 3.
Ce qu'il faut retenir pour le contrôle de qualité est que la distribution normale est symétrique autour de la moyenne [μ], qui est aussi la médiane et s'étale d'autant plus autour de [μ] que l'écart type [σ] est plus grand. Le réglage de la machine est positionné sur la moyenne des pièces
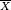
-
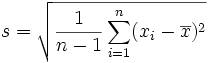
Distribution de Student
Cette distribution, encore appelée loi de Student ou loi t est basée sur la différence entre l'écart type de la population (σ) et celui de l'échantillon (s). Cette différence est d'autant plus grande que l'échantillon est petit si bien que la distribution n'est plus normale lorsqu'on utilise l'écart type de l'échantillon (s) au lieu de l'écart type de la population (σ) .
Le rapport :
suit une distribution de Student. Le paramètre (degré de liberté) représente la précision de l'écart type et détermine la forme de la courbe qui est symétrique, comme la distribution normale. Lorsque le nombre de degrés de libertés augmente, s devient une estimation plus précise de σ.
Distribution du khi-deux
On utilise cette distribution pour comparer deux proportions. En contrôle de réception, ce test, basé sur les probablilités, sert à mettre en évidence si le pourcentage de défectueux entre deux fournisseurs a ou non une signification statistique ou si elle est due au hasard. Comme la distribution de Student, le paramètre 'degré de liberté' donne une distribution de forme différente.
Distribution de Fisher
La distribution de Fisher (F) ou test de Fisher est utilisée en régression et analyse de la variance. F utilise 2 degrés de liberté, un au numérateur (m), l'autre au dénominateur (n).On la note F(m,n)
Distribution de Weibull
La loi de Weibull généralise la loi exponentielle. Elle modélise des durées de vie.
Statistique descriptive
Le contrôle de la qualité utilise un certain nombre de termes techniques : échantillon, population, caractère....explicités dans la statistique descriptive. De même, les critères de position (moyenne, mode, médiane) et de dispersion (étendue, écart-type) sont nécessaires à la compréhension de l'histogramme.
La moyenne arithmétique est le paramètre de position le plus représentatif, car le plus sensible aux fluctuations. Par contre, la médiane et le mode sont plus simples à déterminer, ne nécessitant aucun calcul.
L'estimateur du paramètre de dispersion le plus sensible est l'écart-type basé sur la variation de l'ensemble des valeurs par rapport à la moyenne.
L'étendue, lorsque la taille de l'échantillon est faible (n < 7), est un bon estimateur de la dispersion. Il est utilisé fréquemment dans les cartes de contrôles de mesures.
Estimation par intervalle de confiance
En pratique, on ne peut se fier à l'estimation de paramètres tels que la moyenne ou l'écart-type d'une façon ponctuelle (voir critères de dispersion et erreur (métrologie) sur les mesures). On cherche à trouver un intervalle dans lequel les paramètres inconnus et estimés ont une chance de se situer. C'est le principe de l'estimation par intervalle de confiance.