Analyse de la variance - Définition

Introduction

L'analyse de la variance (terme souvent abrégé par le terme anglais ANOVA : ANalysis Of VAriance) est un test statistique permettant de vérifier que plusieurs échantillons sont issus d'une même population.

Ce test s'applique lorsque l'on mesure une ou plusieurs variables explicatives catégorielles (appelées alors facteurs de variabilité, leurs différentes modalités étant parfois appelées « niveaux ») qui influence sur la distribution d'une variable continue à expliquer. On parle d'analyse à un facteur, lorsque l'analyse porte sur un modèle décrit par un facteur de variabilité, d'analyse à deux facteurs ou d'analyse multifactorielle.

Principe

L'analyse de la variance permet d'étudier le comportement d'une variable à expliquer continue en fonction d'une ou plusieurs variables explicatives catégorielle. Lorsque l'on souhaite étudier le comportement de plusieurs variables à expliquer en même temps, on utilisera une analyse de la variance multiple (MANOVA). Si un modèle contient des variables explicatives catégorielles et continues et que l'on souhaite étudier les lois liant les variables explicatives continues avec la variable à expliquer en fonction de chaque modalité des variables catégorielles, on utilisera alors une analyse de la covariance (ANCOVA).

Modèle

La première étape d'une analyse de la variance consiste à écrire le modèle théorique en fonction de la problématique à étudier. Il est souvent possible d'écrire plusieurs modèles pour un même problème, en fonction des éléments que l'on souhaite intégrer dans l'étude.

Le modèle général s'écrit :

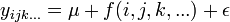
avec Y_ijk... la variable à expliquer, μ une constante, f() une relation entre les variables explicatives et ε l'erreur de mesure. On pose l'hypothèse fondamentale que l'erreur suit une loi normale : ε = N(0,σ²).

Variables explicatives

On distingue deux types de variables catégorielles : avec ou sans effet aléatoire.

Pour une variable à effet fixe, pour chaque modalité, il existe une valeur fixe correspondante. Elles s'écrivent dans le modèle théorique avec une lettre majuscule :

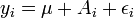
avec A = A₀ pour i=0, A = A₁ pour i=1, etc.

Dans le cas d'une variable à effet aléatoire, la variable est issue d'une loi supposée normale qui s'ajoute à la valeur fixe. Elles s'écrivent dans le modèle théorique avec une lettre grecque minuscule :

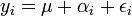
avec α_i = μ_a + ε_α et

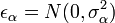
Un modèle basé seulement sur des variables explicatives à effets fixes et effets aléatoires est appelé modèle mixte.

Hypothèses fondamentales

La forme générale de l'analyse de variance repose sur le test de Fisher et donc sur la normalité des distributions et l'indépendance des échantillons.

• Normalité de la distribution : on suppose, sous l'hypothèse nulle, que les échantillons sont issus d'une même population et suivent une loi normale. Il est donc nécessaire de vérifier la normalité des distributions et l'homoscédasticité (homogénéité des variances, par des tests de Bartlett ou de Levene par exemple). Dans le cas contraire, on pourra utiliser les variantes non paramétriques de l'analyse de variance (ANOVA de Kruskal-Wallis ou ANOVA de Friedman).

• Indépendance des échantillons : on suppose que chaque échantillon analysé est indépendant des autres échantillons. En pratique, c'est la problématique qui permet de supposer que les échantillons sont indépendants. Un exemple fréquent d'échantillons dépendants est le cas des mesures avec répétitions (chaque échantillon est analysé plusieurs fois). Pour les échantillons dépendants, on utilisera l'analyse de variance à mesures répétées ou l'ANOVA de Friedman pour les cas non paramétriques.

Hypothèses à tester

L'hypothèse nulle correspond au cas où les distributions suivent la même loi normale.

L'hypothèse alternative est qu'il existe au moins une distribution dont la moyenne s'écarte des autres moyennes :

.

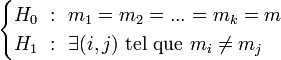
Décomposition de la variance

La première étape de l'analyse de la variance consiste à expliquer la variance totale sur l'ensemble des échantillons en fonction de la variance due aux facteurs (la variance expliquée par le modèle), de la variance due à l'interaction entre les facteurs et de la variance résiduelle aléatoire (la variance non expliquée par le modèle). étant un estimateur biaisé de la variance, on utilise la somme des carrés des écarts (SCE en français, SS pour Sum Square en anglais) pour les calculs et l'estimateur non biaisé de la variance (également appelé carré moyen ou CM).

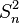
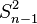
L'écart (sous entendu l'écart à la moyenne) d'une mesure est la différence entre cette mesure et la moyenne :

.

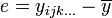
La somme des carrés des écarts SCE et l'estimateur se calculent à partir des formules :

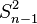
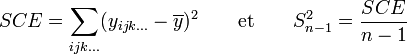
Il est alors possible d'écrire la somme des carrés des écarts total SCE_total comme étant une composition linéaire de la somme des carrés des écarts de chaque variable explicative SCE_factor et de la somme des carrés des écarts pour chaque interaction SCE_interaction :

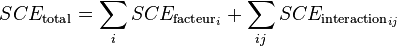
Cette décomposition de la variance est toujours valable, même si les variables ne suivent pas de loi normale.

Test de Fisher

Par hypothèse, la variable observée y_i suit une loi normale. La loi du χ² à k degrés de liberté étant définie comme étant la somme de k lois normales au carré, les sommes des carrés des écarts SCE suivent des lois du χ², avec DDL le nombre de degrés de liberté :

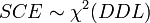
La loi de Fisher est définie comme le rapport de deux lois du χ². Dans le cas de l'hypothèse nulle H₀, le rapport entre deux estimateurs non biaisés de la variance doit donc suivre une Loi de Fisher :

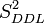
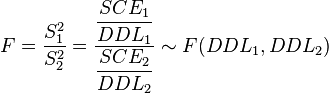
Si la valeur de F n'est pas compatible avec cette loi de Fisher (c'est-à-dire que la valeur de F est supérieure au seuil de rejet), alors on rejette l'hypothèse nulle : on conclut qu'il existe une différence statistiquement significative entre les distributions. Le facteur de variabilité ne sépare pas la population étudiée en groupes identiques. Pour rappel, la valeur de seuil de rejet F_α(DDL₁,DDL₂) est précalculée dans les tables de référence, en fonction du risque de première espèce α et des deux degrés de libertés DDl₁ et DDL₂.

Tests « post-hoc »

L'analyse de variance permet simplement de répondre à la question de savoir si tous les échantillons suivent une même loi normale. Dans le cas où l'on rejette l'hypothèse nulle, cette analyse ne permet pas de savoir quels sont les échantillons qui s'écartent de cette loi.

Pour identifier les échantillons correspondant, on utilise différents tests «post-hoc» (ou tests de comparaisons multiples, MCP pour Multiple Comparison Test). Ces tests obligent en général à augmenter les risques de l'analyse (en termes de risque statistique). Il s'agit d'une généralisation à k populations du test t de Student de comparaison de moyennes de deux échantillons avec ajustement de l'erreur (FDR, FWER, etc.) Par exemple : les tests LSD de Ficher, les tests de Newman-Keuls, les tests HSD de Tukey, les tests de Bonferroni et Sheffé.

Dans la biologie moderne, notamment, des tests MCP permettent de prendre en compte le risque de façon correcte malgré le grand nombre de tests effectués (par exemple pour l'analyse de biopuces).

Pourquoi ne pas faire directement ces tests, sans passer par une analyse de la variance avant ?

Lorsque l'on analyse plusieurs variables explicatives ayant plusieurs modalités chacune, le nombre de combinaison possible devient rapidement très grand.