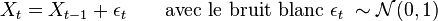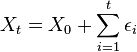Marche aléatoire - Définition

Marche aléatoire continue

Très utilisée dans la modélisation de séries temporelles continues, une marche aléatoire peut s'écrire:

Il s'agit d'un cas particulier d'un processus autorégressif (c'est-à-dire « régressé sur lui-même ») avec ρ = 1. La valeur du paramètre ρ est très importante car elle change fondamentalement la propriété de la série :

• X_t = ρX_{t − 1} + ε_t

De manière récursive, une marche aléatoire est simplement la somme de bruits blancs. On l'écrit:

Pour simuler une marche aléatoire, un petit exemple avec le logiciel de statistique R est montré:

a<-rnorm(100)# crée un vecteur "a" de 100 réalisation d'une loi normale (0,1).

b<-cumsum(a) # Crée un vecteur "b" dont chaque élément correspond à la somme cumulée des éléments de a.

plot.ts(b) #Crée un graphe (le ".ts" est utilisé pour "time series")