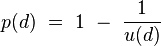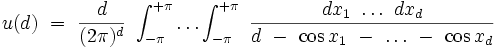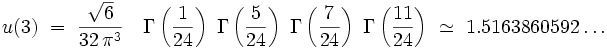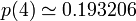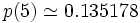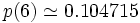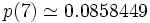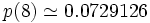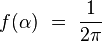Marche aléatoire - Définition

Récurrence et dimensionnalité

Récurrence

Considérons une marche aléatoire isotrope sur le réseau à d dimensions spatiales. On peut toujours choisir de prendre le point de départ de cette marche comme origine O du système de coordonnées cartésiennes. La question de la récurrence consiste alors à se demander si on peut trouver au moins un instant t positif fini pour lequel la particule repasse par l'origine O.

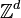
La marche aléatoire sera dite récurrente si et seulement si la probabilité que la particule repasse à l'origine O pour un certain instant t ultérieur fini vaut un.

Théorème de Pólya (1921)

Cette propriété de récurrence dépend fortement de la dimensionnalité de l'espace ; on peut en effet démontrer le théorème (Pólya - 1921) :

• pour d = 1 et d = 2, la marche aléatoire isotrope est récurrente.

• pour d = 3 et au-delà, la marche aléatoire isotrope n'est pas récurrente ; on dit alors qu'elle est transitoire (en bon « franglais », certains auteurs utilisent parfois le mot anglais transient).

Certains disent parfois en plaisantant que ce théorème est au fondement du proverbe : « Tous les chemins mènent à Rome. » Le lecteur notera que, si l'on inclut les chemins « cosmiques », alors le proverbe est faux !

Probabilité de retour à l'origine en dimension supérieure ou égale à trois 

On sait en fait calculer la probabilité que le marcheur, parti initialement de l'origine, revienne à l'origine, et ce pour toutes les dimensions d > 2. Cette probabilité p(d) admet l'expression suivante (Montroll - 1956) :

où u(d) est une intégrale à d dimensions :

Le cas particulier d = 3 avait en fait déjà été obtenu précédemment par Watson, Mc Crea et Whipple, et Domb. L'expression analytique de l'intégrale n'a été obtenue qu'en 1977 par Glasser et Zucker :

où Γ(z) est la fonction Gamma d'Euler. On obtient donc en trois dimension une probabilité de retour à l'origine : , voisine de 34 pour cent.

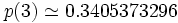
Les expressions analytiques de u(d) ne sont pas connues en dimension d supérieure à trois. On obtient les valeurs numériques suivantes :

• 

• 

• 

• 

• 

Marche aléatoire isotrope sur un continuum à x dimensions

Deux dimensions

On considère la marche aléatoire sur le plan définie par le processus suivant :

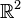
• la particule est initialement à l'origine : x(0)=0, y(0)=0 et se déplace sur le plan par des sauts successifs effectués toutes les secondes.

• à chaque saut, la particule avance d'une longueur unité dans une direction caractérisée par un angle polaire α défini par rapport à l'axe Ox. On choisit par exemple : .

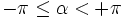
• Cet angle polaire α est une variable aléatoire, caractérisée par une densité de probabilité f(α). Le processus est isotrope lorsque toutes les directions sont équiprobables, ce qui correspond au choix d'une densité uniforme :

Chaque direction de saut est totalement indépendante de la direction du saut précédent.

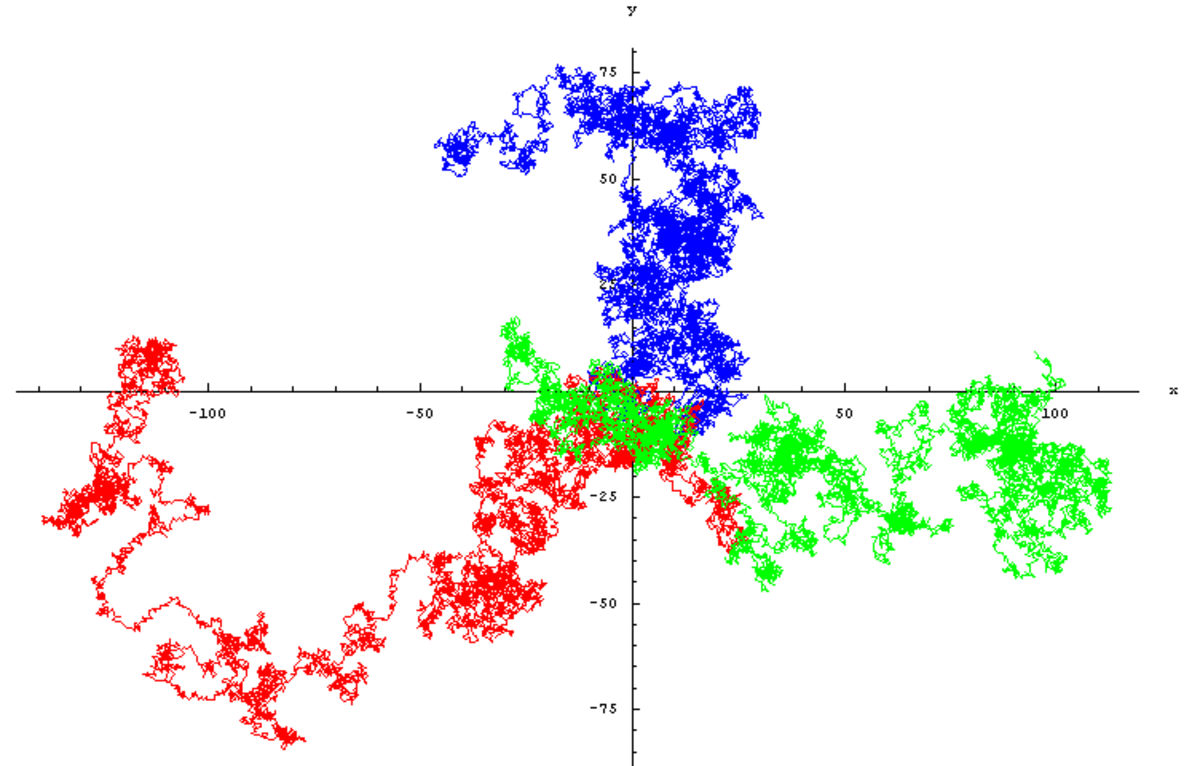
La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les trois trajectoires obtenues.

Spécimens

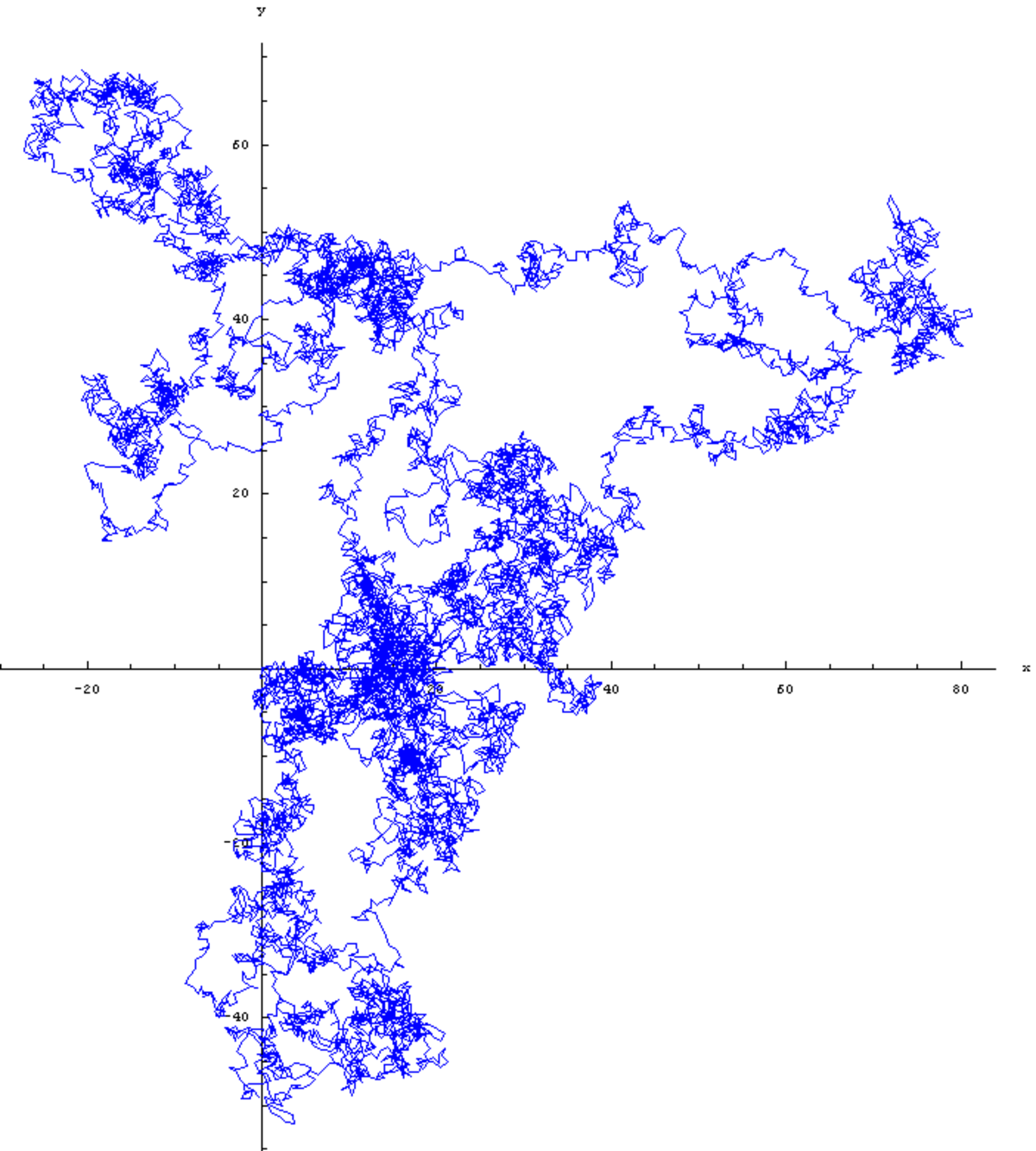
La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le plan après 10 000 pas, partant de l'origine.