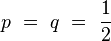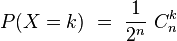Marche aléatoire - Définition

Marche aléatoire isotrope sur un réseau à x dimensions

Deux dimensions

On considère une marche aléatoire sur le réseau plan . Il y a ici quatre mouvements possibles à chaque site : en avant, en arrière, à droite, à gauche. La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les trois trajectoires obtenues.

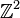
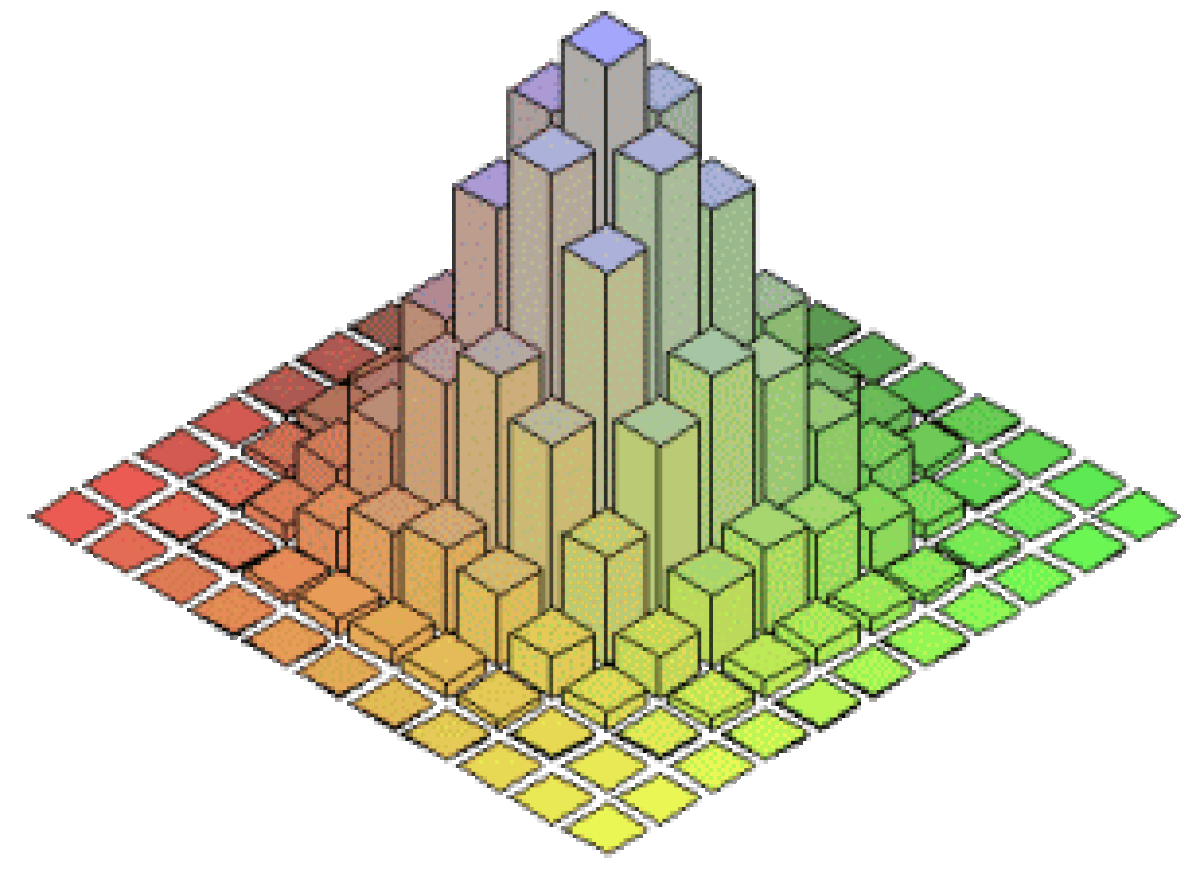
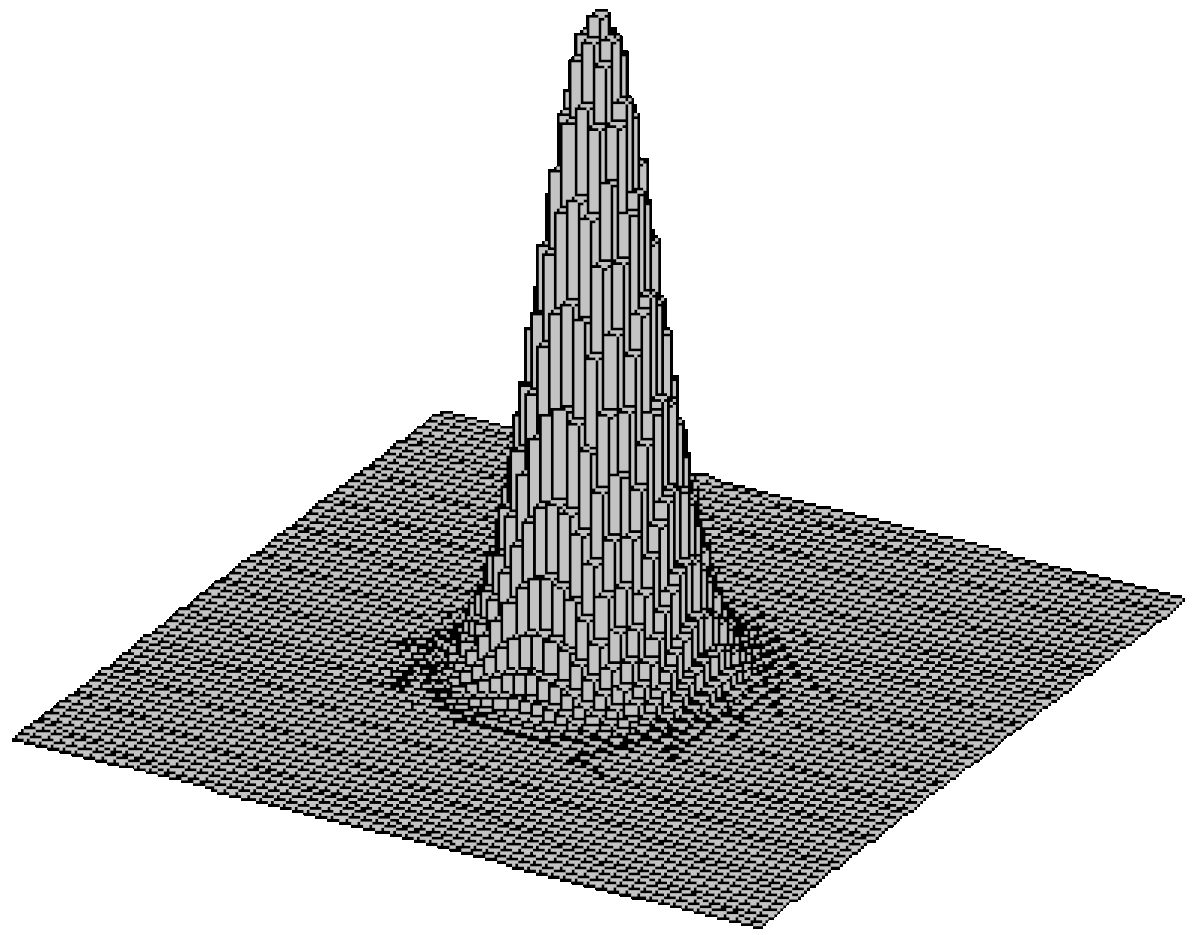
Pour des longues marches, la distribution de la position finale du marcheur se comporte asymptotiquement comme une distribution gaussienne. Cette convergence est illustrée ci-dessous : on trace les répartitions des probabilités de présence sur le réseau après 10 pas, puis après 60 pas :

Spécimens

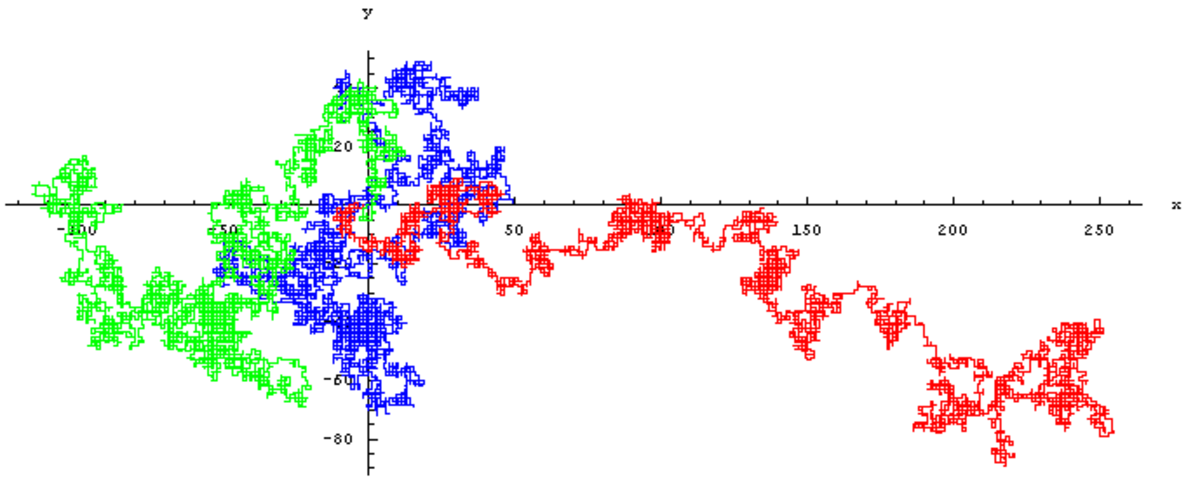
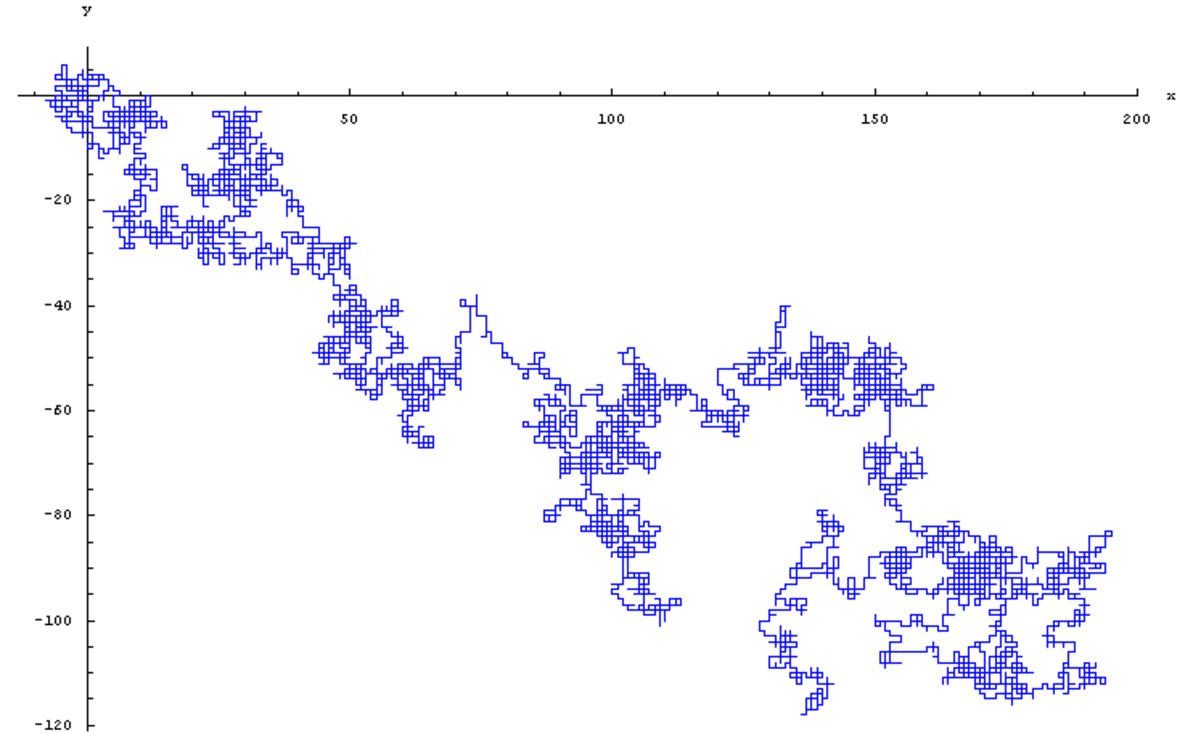
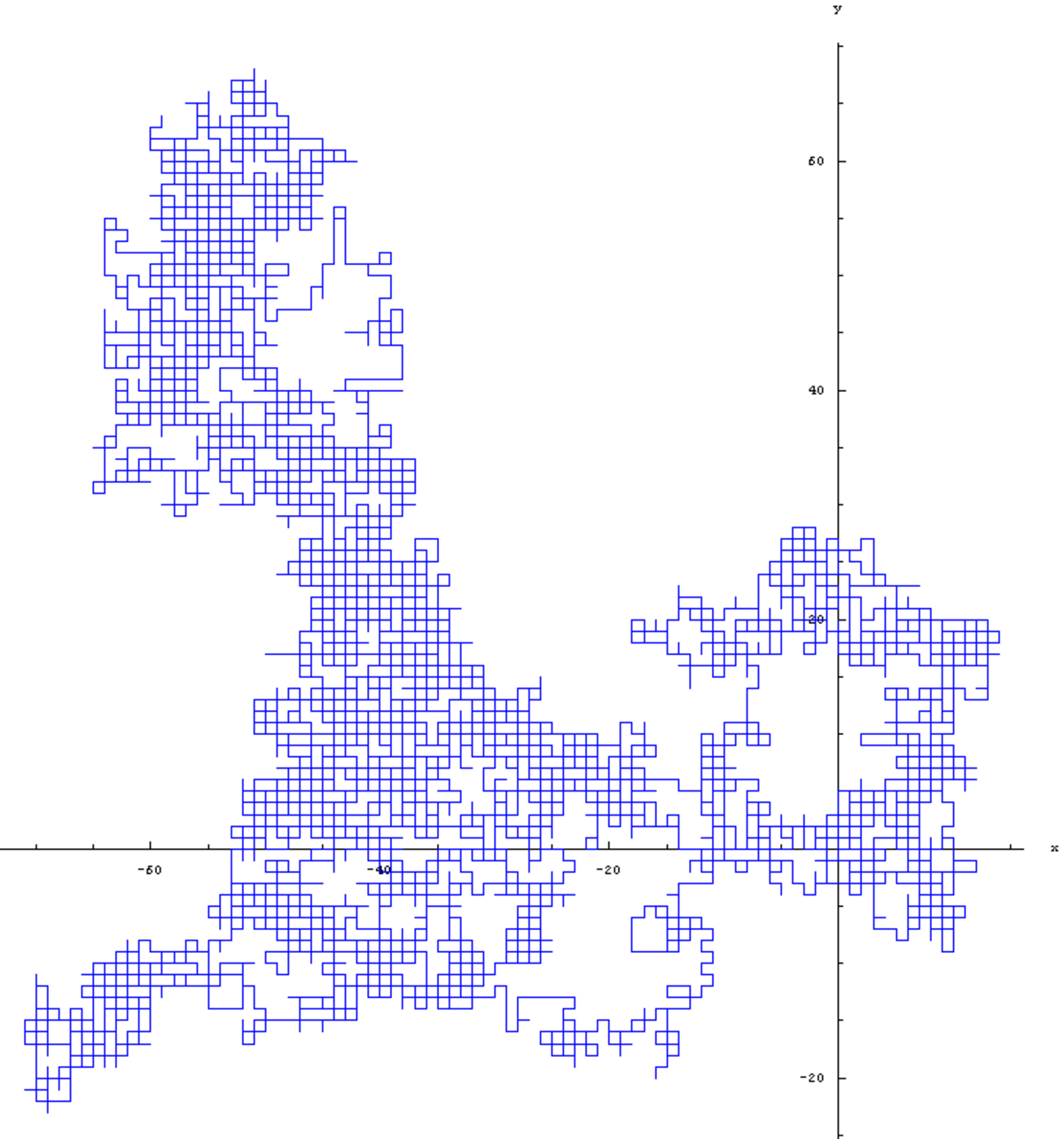
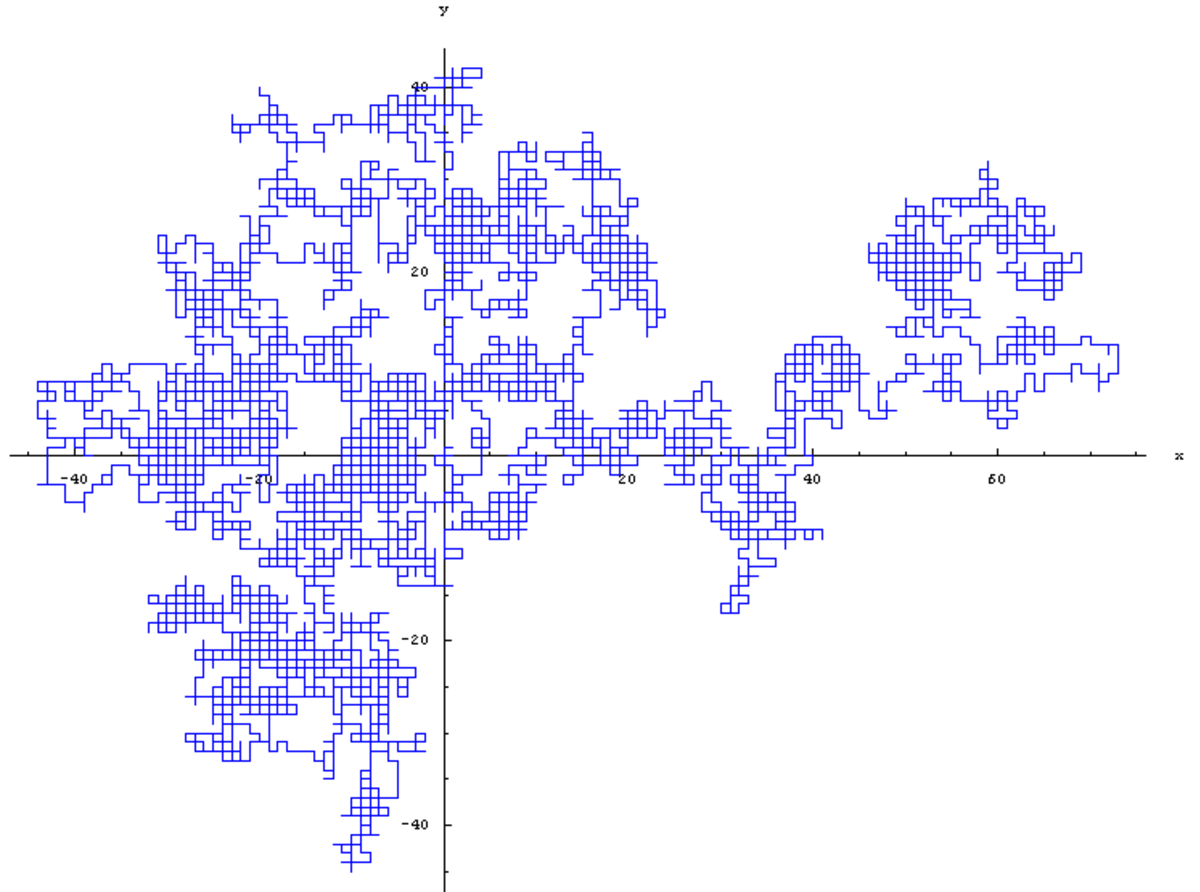
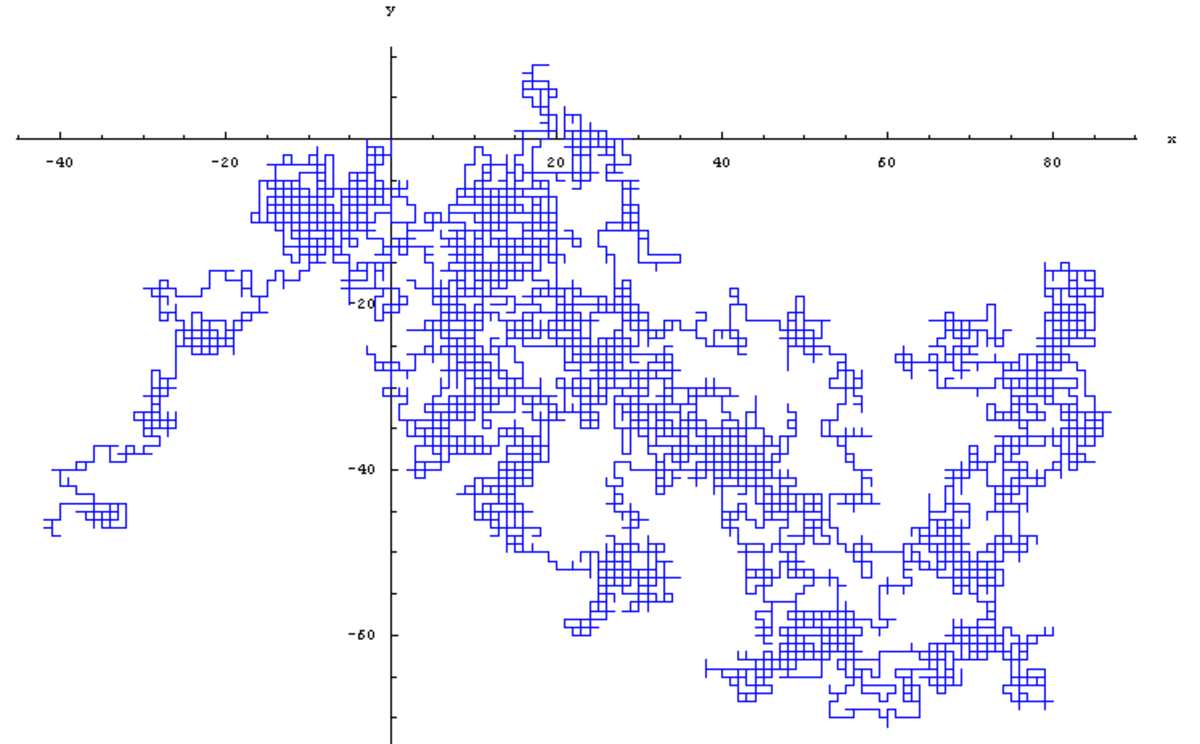
La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le réseau après 10 000 pas, partant de l'origine.

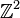
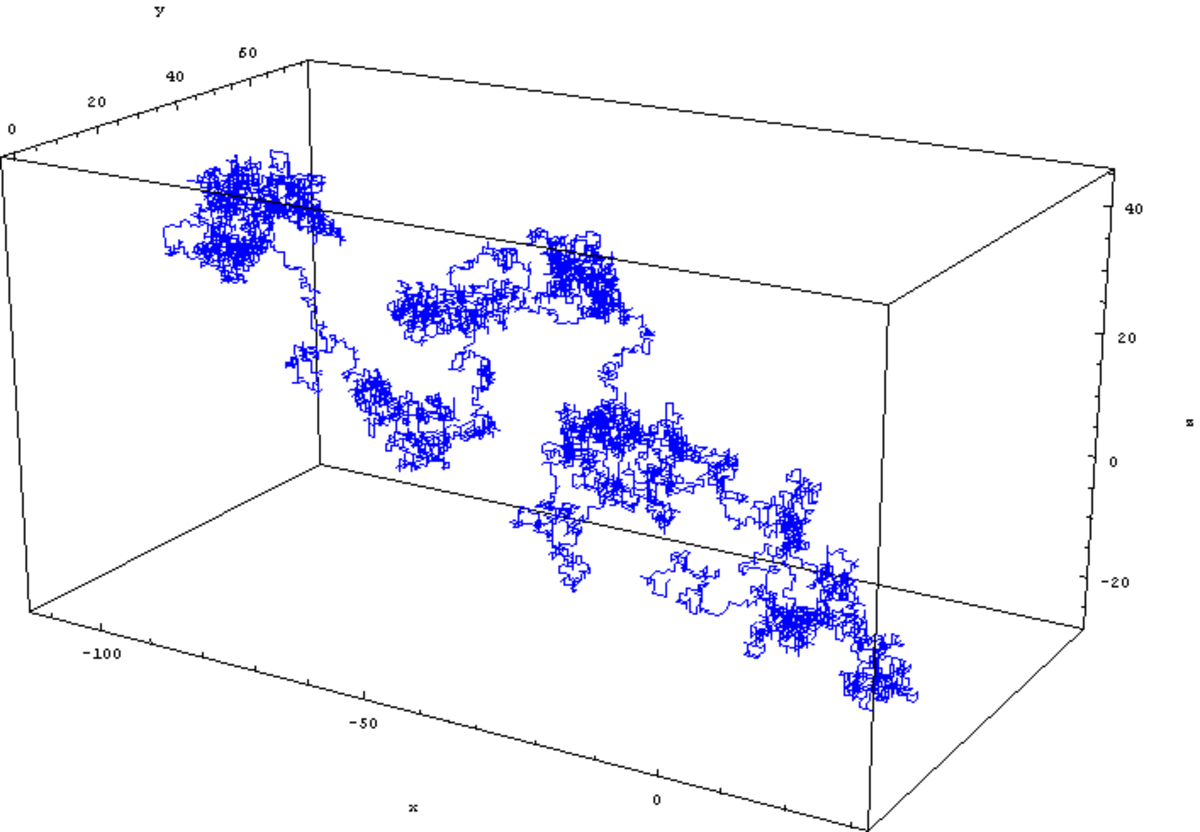
Trois dimensions

On considère une marche aléatoire sur le réseau cubique . Il y a ici six mouvements possibles à chaque site : en avant, en arrière, à droite, à gauche, en haut, en bas.

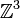
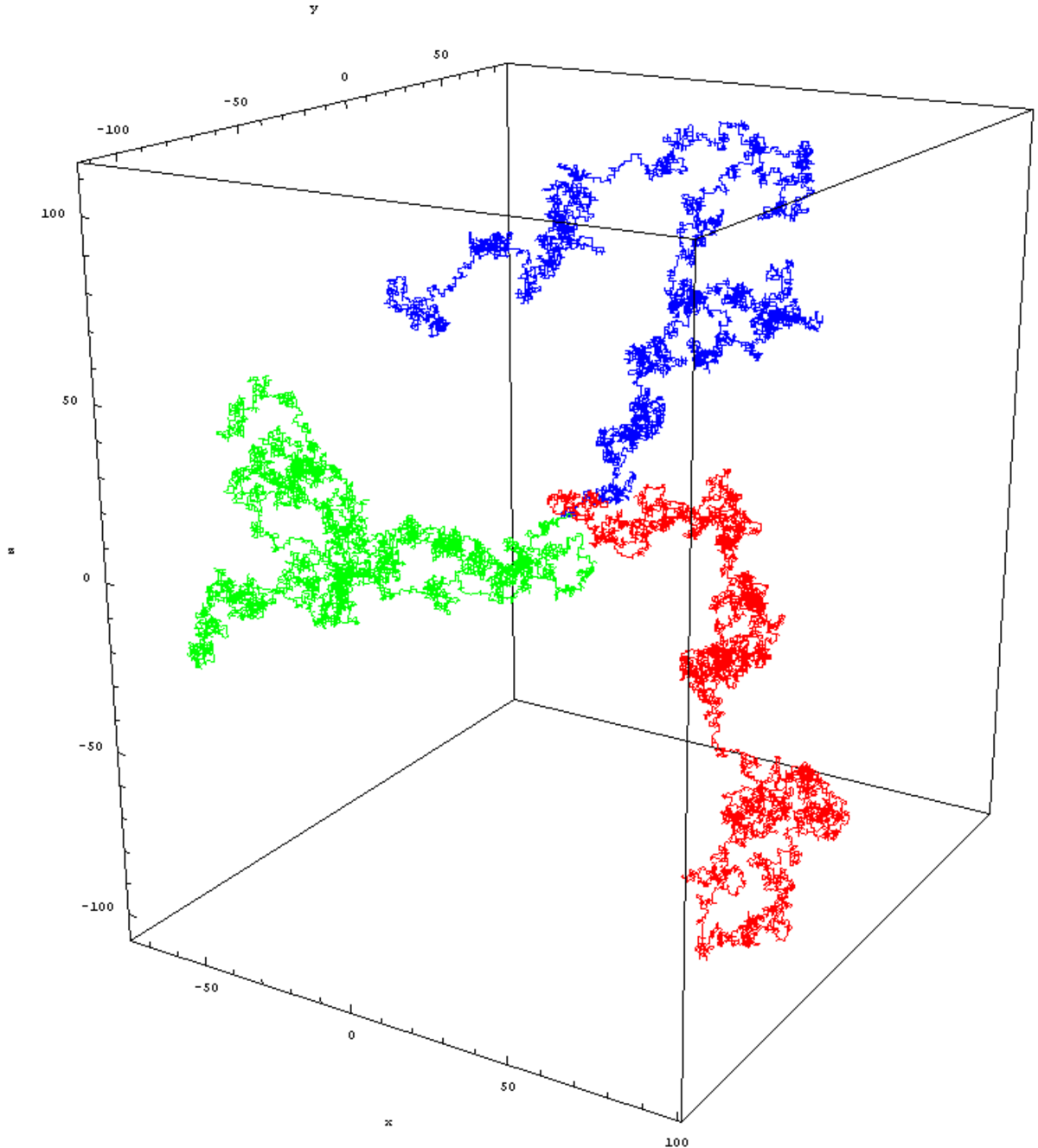
La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les trois trajectoires obtenues.

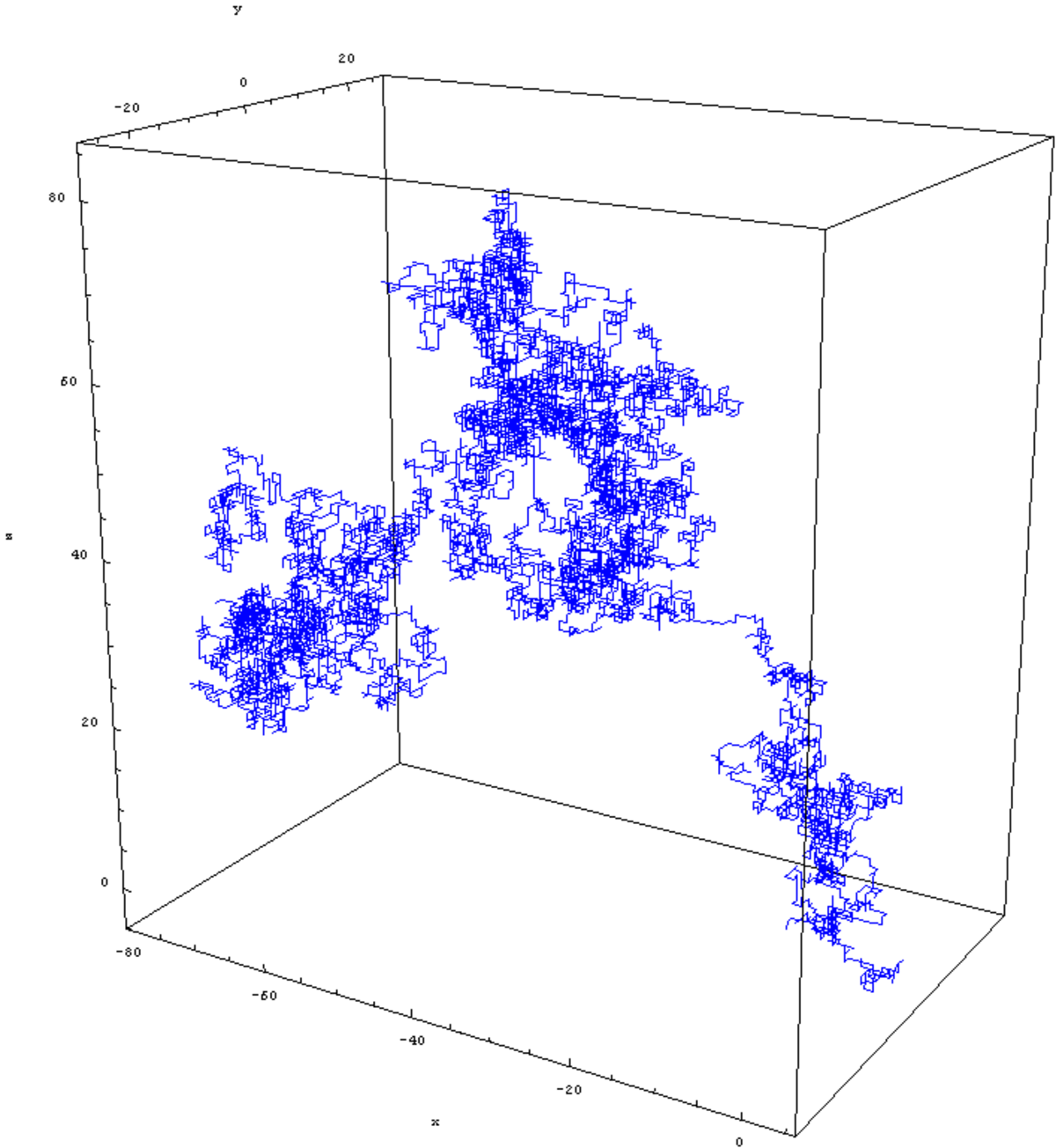
Spécimens

La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le réseau après 10 000 pas, partant de l'origine.

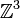
Projections bidimensionnelles

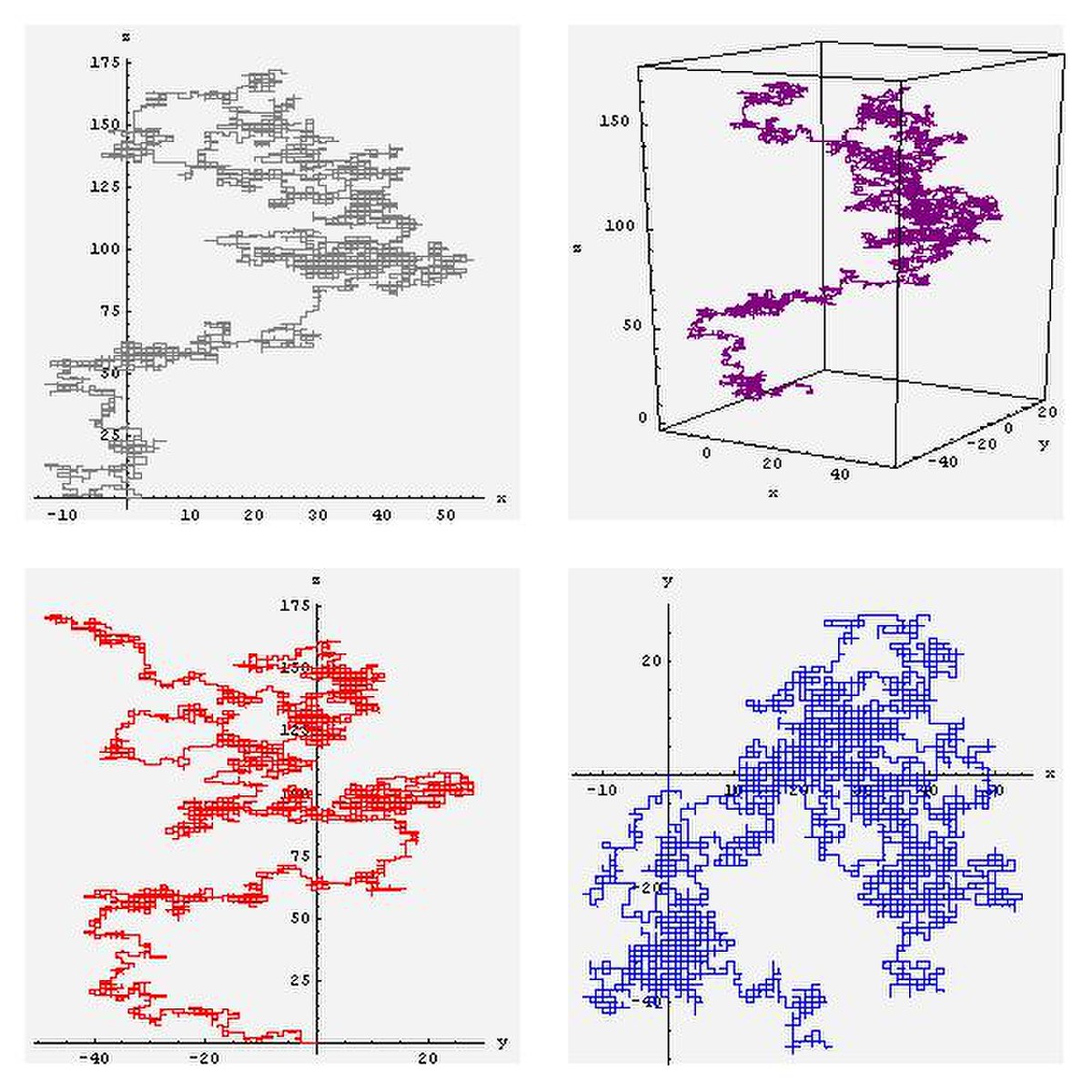
Marche aléatoire discrète à une dimension

Définition

Le modèle de marche aléatoire le plus simple est celui de la marche aléatoire discrète à une dimension sur le réseau périodique . Pour en former un exemple concret, on peut imaginer un individu (ou « particule ») sur un escalier, qui tire à pile ou face pour décider si le prochain pas sera vers le haut ou vers le bas. À chaque étape, il n'y a que deux choix possibles : sur cet exemple, un pas en avant ou un pas en arrière. Le seul paramètre libre du problème est un nombre réel p tel que : 0 < p < 1. L'interprétation physique de ce paramètre est la suivante :

• p représente la probabilité que la particule fasse un saut en avant à chaque instant.

• q = 1 - p représente la probabilité que la particule fasse un saut en arrière à chaque instant.

Le cas le plus simple, qui correspond par exemple au mouvement brownien, consiste à faire l'hypothèse d' isotropie spatiale. Les directions « avant / arrière » de l'espace physique étant a priori équivalentes, on pose l' équiprobabilité :

Il est remarquable que les lois mises en évidence dans ce cas s'étendent à des problèmes de marches aléatoires beaucoup plus complexes.

Marche aléatoire isotrope

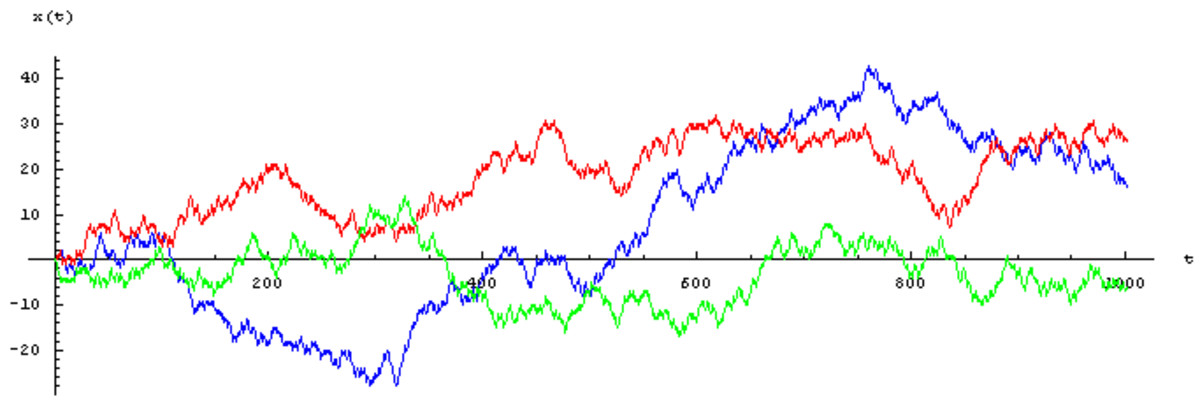
Chacun des tirs au hasard pour choisir le mouvement constitue une épreuve de Bernoulli avec issues équiprobables : ici la probabilité de montée ou de descente est 1/2.

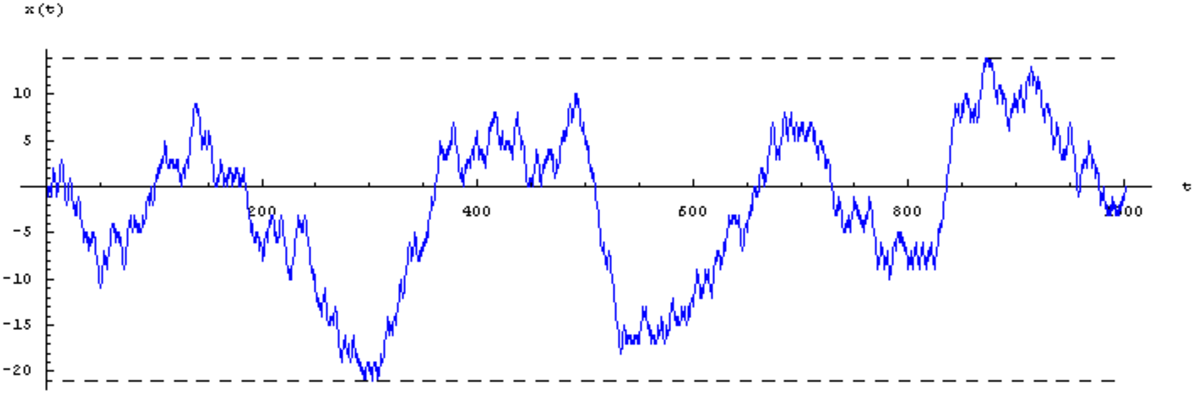
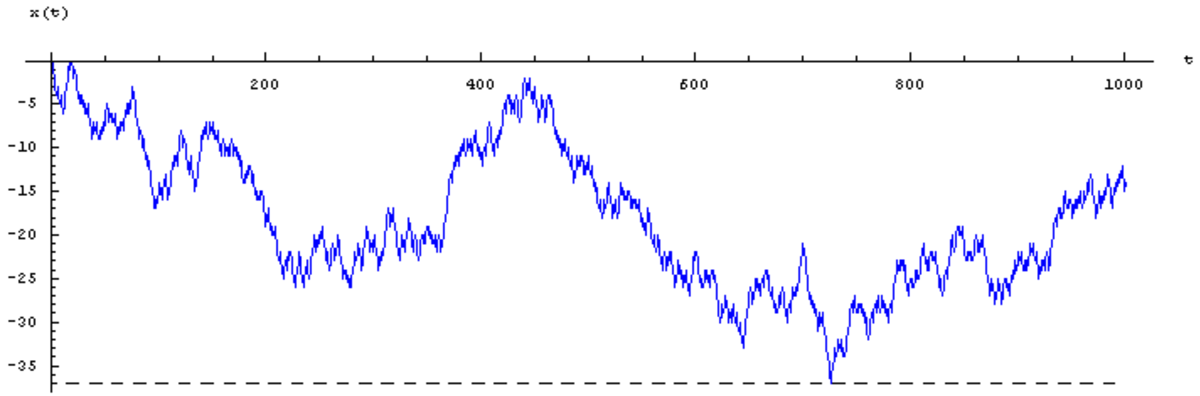
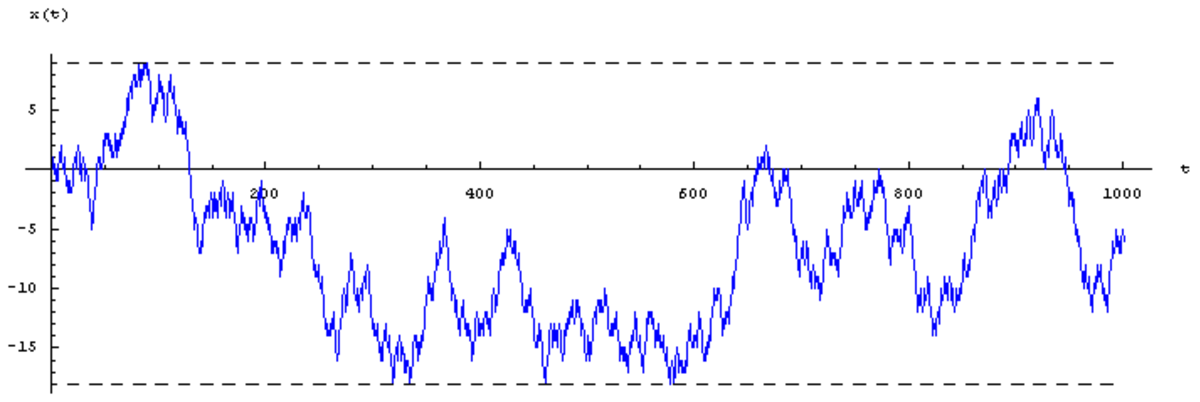
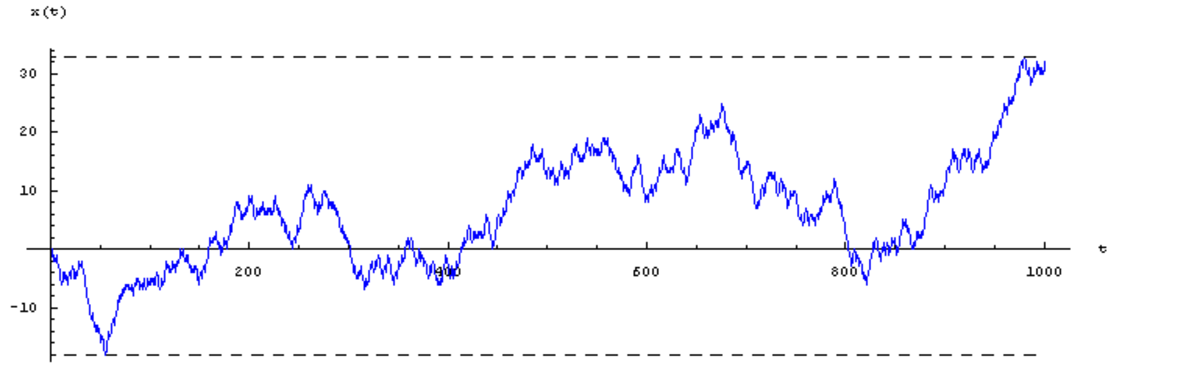
La figure ci-contre montre un échantillon de trois simulations numériques indépendantes de marches aléatoires pour une particule : on a tracé les positions successives x(t) de la particule aux instants t = 1, 2, ..., partant de la condition initiale x(0)=0.

Après n pas, le nombre X de fois où on a tiré "pile" suit la loi binomiale B(n,1 / 2), telle que la probabilité vaut :

où est le nombre de combinaisons de k éléments pris parmi n.

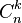
On peut relever la position en prenant la valeur 0 pour la marche initiale, en ajoutant 1 pour chaque pas en avant (pile), en retranchant 1 pour chaque pas en arrière (face). Alors la position Y est donnée par : Y = X - (n-X) = 2X - n. Par rapport à la loi binomiale classique il suffit donc de décaler les résultats de n/2 et de multiplier par 2, ainsi :

• l'espérance est nulle ;
• la variance vaut n et l'écart type  ;
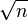
• on a toujours l'inégalité de Bienaymé-Tchebychev ;
• et la loi des grands nombres.

Concrètement, si on renouvelle l'expérience avec un grand nombre de participants, et si on les laisse évoluer pendant un nombre de pas assez important (de l'ordre de n = 100 par exemple) on s'attend à ce que le nuage des positions finales soit en gros centré sur la marche initiale. Ceci peut être rendu quantitatif : en se plaçant dans le régime asymptotique , on démontre en utilisant la formule de Stirling que la loi binomiale se comporte asymptotiquement comme une distribution gaussienne. On obtient notamment un ordre de grandeur de l'étalement du nuage de participants : par exemple on s'attend à ce que 95 % environ des participants soient restés à 20 pas ou moins de la position initiale ( ).

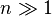
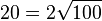
Spécimens

La galerie ci-dessous contient quatre spécimens de marches aléatoires isotropes sur le réseau après 1 000 pas, partant de l'origine. Les lignes en pointillés indiquent respectivement les valeurs maximum et minimum de la position atteintes (après 1000 pas).