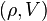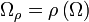Opérateur de Casimir - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus spécifiquement en algèbre, l'opérateur de Casimir est un opérateur particulier. Plus précisément, étant donné une algèbre de Lie munie d'une forme bilinéaire non-dégénérée et invariante, et une représentation de dimension finie, l'opérateur de Casimir est une application linéaire continue particulière sur l'espace vectoriel de la représentation. Cet opérateur commute avec la représentation. Pour l'algèbre de Lie et la représentation étudiées, cet opérateur joue le rôle du laplacien.
Il y a un opérateur de Casimir par représentation, mais il n'y a qu'un opérateur de Casimir pour l'algèbre enveloppante de l'algèbre de Lie. Il n'y a pas de procédure générale pour déterminer les opérateurs de Casimir associés à une algèbre de Lie quelconque, comme il n'y a pas de procédure générale pour déterminer toutes ses représentations, toutefois, on peut en déterminer le nombre (fini ou non) et le rang (théorème de Racah).
En mathématiques, l'opérateur de Casimir a aidé à déterminer les représentations irréductibles d'une algèbre et d'un groupe de Lie, ainsi que les algèbres et groupes de Lie simples. En physique quantique, l'opérateur de Casimir a aidé à mieux connaitre les opérateurs agissant sur la fonction d'onde, et les invariants associés qui sont des nombres quantiques : la masse, le spin, l'isospin en sont des exemples.
L'opérateur de Casimir doit son nom à Hendrik Casimir, son découvreur pour le groupe de Lorentz au début des années 1930.
Formes bilinéaires non-dégénérées et invariantes
Soit
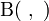
![\ ad_X(Y) = [X,Y]](https://static.techno-science.net/illustration/Definitions/autres/a/ae29a34dfa886ede8335ad43340b17cd_b96b7c6bce43771a778b4a737fb03b47.png)
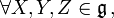
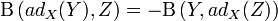
ou encore
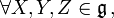
![\Beta \left( \left[ X,Y \right],Z \right) = - \Beta \left( Y ,\left[ X,Z \right] \right)](https://static.techno-science.net/illustration/Definitions/autres/3/33783fbb20419ff517ed038bd4b03783_570de32d60f647ffa9c4e08b9dbee28a.png)
Dans le cas d'une algèbre de Lie associée à un groupe de Lie connexe G, on démontre (par différentiation) que cette invariance est équivalente à l'invariance par l'action
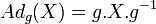
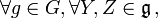
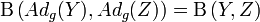
- Exemples
- Sur une algèbre de Lie semi-simple, une forme utilisable est la forme de Killing.
- Sur l'algèbre de Lie associée à un groupe de Lie compact G, il existe une forme bilinéaire non-dégénérée et invariante construite à l'aide de la mesure de Haar
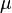
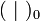
- Sur une sous-algèbre de Lie
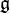
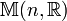
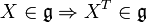
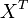
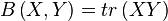
Propriétés
- Indépendance vis-à-vis de la base utilisée : si
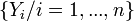
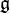
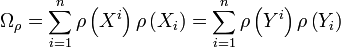
- Commutation avec la représentation : on sait que par définition
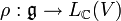
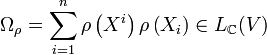
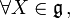
![\left[ \Omega_{\rho} , \rho (X) \right] = 0](https://static.techno-science.net/illustration/Definitions/autres/a/a581f962174a47af2af6fddfa93da457_8776bf1b94ac3dd7739abe880cdf425e.png)
- Si
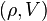
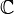
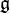
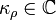
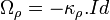
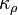
Définitions
Soit
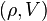
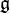
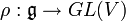
Première définition : Soit
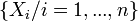
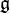
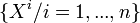
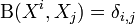
L'opérateur de Casimir est défini par :
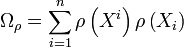
Une deuxième définition, qui n'utilise pas explicitement de la base duale tout en l'introduisant sans le dire, est :
en posant
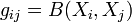
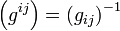
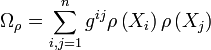
Une troisième définition introduit d'abord l'opérateur de Casimir
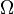
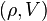
Dans ce cas, l'opérateur de Casimir est défini par :
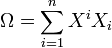
et on retrouve l'opérateur associé à la représentation