Matrice aléatoire - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Quelques ensembles de matrices aléatoires - Articles liés - Applications de la théorie des matrices aléatoire - Bibliographie

Introduction

Une matrice aléatoire est une matrice dont les éléments sont des variables aléatoires.

Face à la complexité croissante des spectres nucléaires observés expérimentalement dans les années 1950, Wigner a suggéré de remplacer l'opérateur hamiltonien du noyau par une matrice aléatoire. Cette hypothèse féconde a conduit au développement rapide d'un nouveau champ de recherche très actif en physique théorique, qui s'est propagé à la théorie des nombres en mathématiques, avec notamment une connexion intéressante avec la fonction zêta de Riemann. En plus de ces exemples on compte parmi les applications de la théorie des matrices aléatoires les systèmes intégrables, le chaos quantique, la gravité quantique en deux dimensions et plus via la théorie des cordes, la QCD sur réseau, les théories de jauge supersymétriques.

Quelques ensembles de matrices aléatoires

Ensembles gaussiens

Ce sont les ensembles introduits par Wigner pour la théorie des spectres nucléaires. On distingue trois ensembles :

l'ensemble gaussien orthogonal pour les systèmes invariants par renversement du temps (GOE),
l'ensemble gaussien unitaire pour les systèmes non-invariants par renversement du temps (GUE),
et l'ensemble gaussien symplectique pour les systèmes avec spin (GSE).

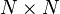
Dans le cas de l'ensemble GOE, on considère des matrices symétriques réelles $N\times N$ dont les élements de matrices $A i j$ obéissent à la distribution gaussienne :

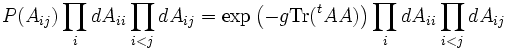
$P(A_{ij})\prod_i dA_{ii} \prod_{i<j} dA_{ij} = \exp\left(-g \mathrm{Tr}({}^t A A)\right) \prod_i dA_{ii} \prod_{i<j} dA_{ij}$

La distribution est invariante par les transformations orthogonales. De même, dans l'ensemble unitaire, on considère des matrices hermitiennes, et la distribution est invariante par les transformations unitaires. Dans l'ensemble GSE, la distribution est invariante sous l'action des transformations symplectiques.

Wigner a déduit la distribution des valeurs propres de ces matrices dans la limite $N \to \infty$ . C'est la loi du demi-cercle.

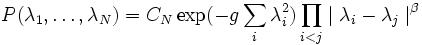
Il est possible de déduire la loi de distribution jointe des valeurs propres par un changement de base. Le résultat est que : $P(\lambda_1,\ldots,\lambda_N) = C_N \exp(-g \sum_i \lambda_i^2) \prod_{i<j} \mid \lambda_i -\lambda_j \mid^\beta$ où les $λ i$ sont les valeurs propres de la matrice, et $β = 1$ dans le cas GOE, $β = 2$ dans le cas GUE, $β = 4$ dans le cas GSE.

A partir de ces distributions, on peut obtenir la loi de distribution des écarts entre valeurs propres. On montre que si $s$ est la distance (normalisée par la densité d'états) entre deux valeurs propres, la probabilité que deux valeurs propres soient distantes de $s$ tend vers zéro si $s$ tend vers zéro. Si les valeurs propres étaient uniformément distribuées, cette probabilité serait donnée par la loi de Poisson et ne tendrait pas vers zéro pour $s$ tendant vers zéro. Cette propriété des ensembles gaussiens est appelée répulsion des niveaux.

Ensembles unitaires

Notés COE, CUE, CSE. Cette fois, les matrices sont respectivement orthogonales, unitaires ou symplectiques. Leurs valeurs propres sont des nombres complexes de module 1. F. J. Dyson a montré que l'étude de la distribution de ces valeurs propres se ramenait à l'étude de la mécanique statistique d'un gaz de particules sur un cercle avec une interaction logarithmique avec la distance.

v · d · m Articles en rapport avec les matrices
Par forme	carrée • triangulaire • diagonale • tridiagonale • élémentaire • échelonnée • creuse • aléatoire • circulante • de Hankel • de Toeplitz • de Vandermonde
Transformée	transposée • adjointe • inverse • Comatrice
En relation	équivalente • semblable • congruente
Par propriété	inversible • diagonalisable • trigonalisable • symétrique • antisymétrique • hermitienne • normale • orthogonale • unitaire • symplectique • de Hadamard • positive • définie positive • à diagonale dominante • nilpotente
Par famille	identité • de De Casteljau • de Cartan • de Hilbert • de Mueller • de Pauli • de Dirac
Particulière	CKM
Associée	de permutation • de passage • compagnon • de Sylvester • d'adjacence • laplacienne • hessienne • jacobienne • génératrice • de contrôle • de corrélation • de Gram • de variance-covariance • d'inertie • de Jones • des gains • stochastique
Résultats	décompositions : LU • QR • polaire • valeurs singulières Trigonalisation • Réduction de Jordan • facteurs invariants
Voir aussi	Théorie des matrices • Algèbre linéaire • Algèbre bilinéaire