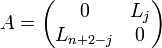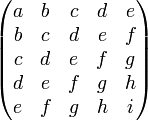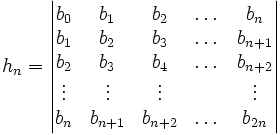Matrice de Hankel - Définition

Introduction

En algèbre linéaire une matrice de Hankel, du nom du mathématicien Hermann Hankel, est une matrice carrée dont les valeurs sont constantes le long des diagonales ascendantes, c'est-à-dire dont les indices vérifient la relation a_i,j = a_{i − 1,j + 1}

Par exemple une matrice de Hankel de taille 5 s'écrit sous la forme

Cette matrice a une certaine parenté avec les matrices de Toeplitz (ces dernières sont des matrices de Hankel renversées).

Sur un espace de Hilbert muni d'une base hilbertienne, on peut définir plus généralement un opérateur de Hankel. Ce dernier admet pour représentation une matrice de Hankel infinie, c'est-à-dire que le coefficient a_i,j = (e_i | a(e_j)), dépend seulement de i + j.

Déterminant et transformation de Hankel

À toute suite (b_n) on peut associer la suite des déterminants h_n des matrices de Hankel successives

• une suite est nulle si et seulement si sa transformée de Hankel est nulle

• une suite vérifie une relation de récurrence linéaire à coefficients constants si et seulement si la transformée de Hankel est nulle à partir d'un certain rang.

Éléments propres dans un cas particulier

Un cas particulier de matrices de Hankel est celui de matrices anticirculantes, lorsque b_{n + j} = b_{j − 1}.

Dans ce cas, on peut aisément diagonaliser les matrices de Hankel : On considère la base de diagonalisation des matrices circulantes de taille n ; on note P la matrice de passage associée d'élements générique w^{(i − 1)(j − 1)} où est une racine n − ième, primitive, de l'unité. On note C_j ses colonnes.

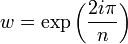
Si M est une marice de Hankel, on note M' = P ^{− 1}MP. On remarque que M'C₁ = LC₁, où est la somme des coefficients de chaque ligne.

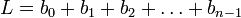
Si n est pair, -1 est racine n-ième de l'unité, le vecteur colonne est et

, où est la somme alternée des coefficients de chaque ligne.

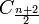
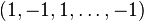
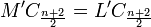
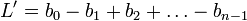
Si , on voit que M'C_j = L_jC_{n + 2 − j} où  ; la valeur en w^{j − 1} du polynôme associé : .

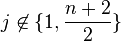
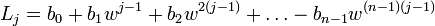
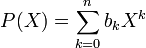
On remarque que le plan Vect(C_j,C_{n + 2 − j}) est stable sous l'action de l'endomorphisme canoniquement associé à M ; la restriction à cet espace,de l'endomorphisme (complexe) associé, a pour matrice dans la base des deux colonnes (C_j,C_{n + 2 − j}) :  ; on en déduit M', puis une diagonalisation de M.