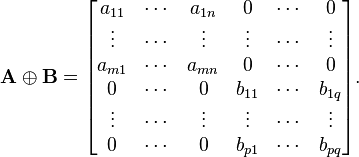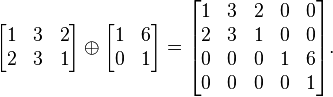Matrice par bloc - Définition
La liste des auteurs de cet article est disponible ici.
Produit direct
De manière similaire à la somme directe, il existe une opération appelée produit direct portant sur les matrices par blocs.
Somme directe
Pour toutes matrices arbitraires A (de taille m × n) et B (de taille p × q), il existe une somme directe de A et B', notée A
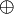
Par exemple,
Cette opération est généralisable naturellement à tous tableaux de dimensions arbitraires (pourvu que A et B aient le même nombre de dimensions).
Notons que tout élément dans la somme directe de deux espaces vectoriels matriciels peut être représentée comme une somme directe de matrices.
Application
En algèbre linéaire, l'utilisation d'une matrice par bloc correspond à avoir une application linéaire pensée en termes de groupes correspondants à des vecteurs de base. Cela rejoint l'idée d'avoir des décompositions en sommes directes distinctes des ensembles de définitions de départ et d'arrivée. Cela est particulièrement significatif si un bloc est une matrice nulle ; ceci indique qu'un sous-ensemble est linéaire à une sous-somme. Étant donné cette interprétation par des applications linéaires et des sommes directes, il existe un genre spécial de matrice par bloc pour les matrices carrées (où m=n). Dans ce cas, on peut postuler une interprétation de ce type de matrice comme un endomorphisme d'un espace de dimension n V ; la structure par bloc dans lesquels les blocs sont disposés en lignes et colonnes est importante car elle correspond à obtenir une décomposition en somme directe simple (au lieu de deux) sur V. Dans ce cas, par exemple, les blocs diagonaux les plus évidents sont tous carrés. Ce type de structure est nécessaire pour la description de la réduction de Jordan.
Cette technique est utilisée pour alléger les calculs sur les matrices, les développements en colonnes et lignes, et autres applications en informatique, y compris la conception de puce d'intégration à très grande échelle. L'algorithme de Strassen pour des produits matriciels rapides, comme le code de Hamming (7,4) pour la détection d'erreur et la récupération de données dans les transmissions de données.