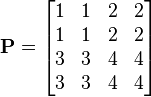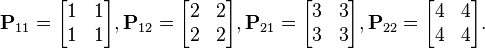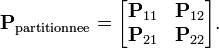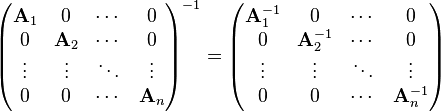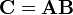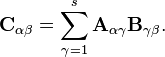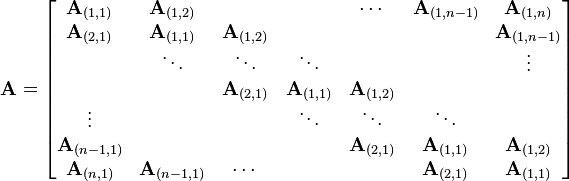Matrice par bloc - Définition

Introduction

En théorie des matrices, une matrice par bloc ou matrice partitionnée est une matrice pouvant être divisée en matrices rectangulaires de dimensions inférieures appelées blocs. On peut dire également que la matrice est écrite en termes de matrices mises côte à côte. Une matrice par bloc doit se conformer à une manière cohérente de division des lignes et des colonnes : on groupe les lignes en « groupes » adjacents, et les colonnes de la même manière. La partition se fait dans les rectangles décrits par un groupe de lignes adjacentes croisant un groupe de colonnes adjacentes. En d'autres termes, la matrice est divisée par certaines des lignes horizontales et verticales la traversant.

Exemple

La matrice

peut être partitionnée en quatre blocs 2×2

On peut alors écrire la matrice par bloc comme :

Matrices par blocs diagonales

Une matrice bloc-diagonale (ou diagonale par blocs) est une matrice carrée qui possède des blocs matrices carrées sur la diagonale principale, tels que les blocs non-diagonaux soient des matrices nulles. Une matrice bloc-diagonale A est de forme :

où A_k est une matrice carrée ; en d'autres termes, c'est la somme directe de A₁, …, A_n. On peut aussi noter ceci : A₁   A₂   A_n  ou  diag(A₁, A₂, , A_n), ce dernier étant une expression dans le même formalisme que celui d'une matrice diagonale). Toute matrice carrée peut être de manière triviale considérée comme une matrice bloc-diagonale avec un seul bloc.

Pour le déterminant (mathématiques) et la trace, les expressions sont alors :

),

).

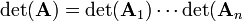
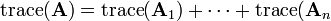
L'inverse d'une matrice diagonale par blocs est la matrice, diagonale par blocs, des inverses des blocs :

Multiplication de matrices par blocs

Un produit de matrices par blocs peut être effectué en considérant seulement des opérations sur les sous-matrices. Étant données une matrice avec q partitions de lignes et s de colonnes :

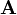
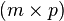
et une matrice avec s partitions de lignes et r partitions de colonnes :

,

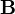
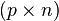
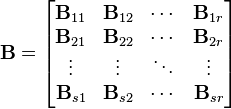
le produit matriciel :

peut être effectué par bloc, donnant , matrice avec q partitions de lignes et r partitions de colonnes. Les blocs sous-matrices de sont calculés de la manière suivante :

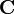
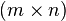
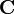
Matrices de Toeplitz par blocs

Une matrice de Toeplitz par bloc est une autre matrice par bloc spéciale, contenant des blocs répétés le long des diagonales de la matrice, comme pour les coefficients d'une matrice de Toeplitz. Une matrice de Toeplitz par bloc A est de la forme :

Matrices tridiagonales par blocs

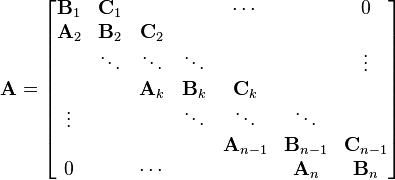
Une matrice tridiagonale par bloc est une autre matrice par bloc spéciale, qui est comparable à la matrice diagonale par bloc, c'est-à-dire une matrice carrée ayant des matrices blocs carrées sur les diagonales principales, inférieure et supérieure, les autres blocs étant des matrices nulles. C'est une matrice tridiagonale essentiellement, mais qui possède des sous-matrices à la place des coefficients scalaires. Une matrice tridiagonale par bloc A a la forme :

où A_k, B_k et C_k sont des sous-matrices carrées sur les diagonales inférieure, principale et supérieure respectivement.

Les matrices tridiagonales par blocs sont parfois rencontrées dans les solutions numériques des problèmes d'ingénierie (comme par exemple en mécanique des fluides numérique). Les méthodes numériques optimisées pour une factorisation LU sont disponibles ainsi que des algorithmes de résolution de systèmes d'équations avec une matrice tridiagonale par bloc pour matrice de coefficients. L'algorithme de Thomas, utilisé pour obtenir une solution efficace des systèmes d'équations impliquant une matrice tridiagonale peut être aussi appliqué en utilisant des opérations matricielles aux matrices tridiagonales par blocs (voir aussi décomposition LU par bloc).