Méthode du dynamique et du funiculaire - Définition

Explication

Le funiculaire est en fait un treillis dont les nœuds sont sur les droites d'action des forces.

Pour qu'un solide soit en équilibre, il faut

1. Que la somme des forces soit nulle, et
2. Que la somme des moments de forces par rapport à un point quelconque soit nulle.

Ce qui importe pour le moment, c'est la hauteur du point considéré à la droite portant la force, dite ligne d'action de la force ; c'est la longueur du segment perpendiculaire à la ligne d'action passant par le point. Dans le cadre de la statique, on peut donc placer le point d'application de la force n'importe où sur cette droite d'action (ceci devient faux lorsque l'on considère les déformations ou les notions d'équilibre stable ou instable).

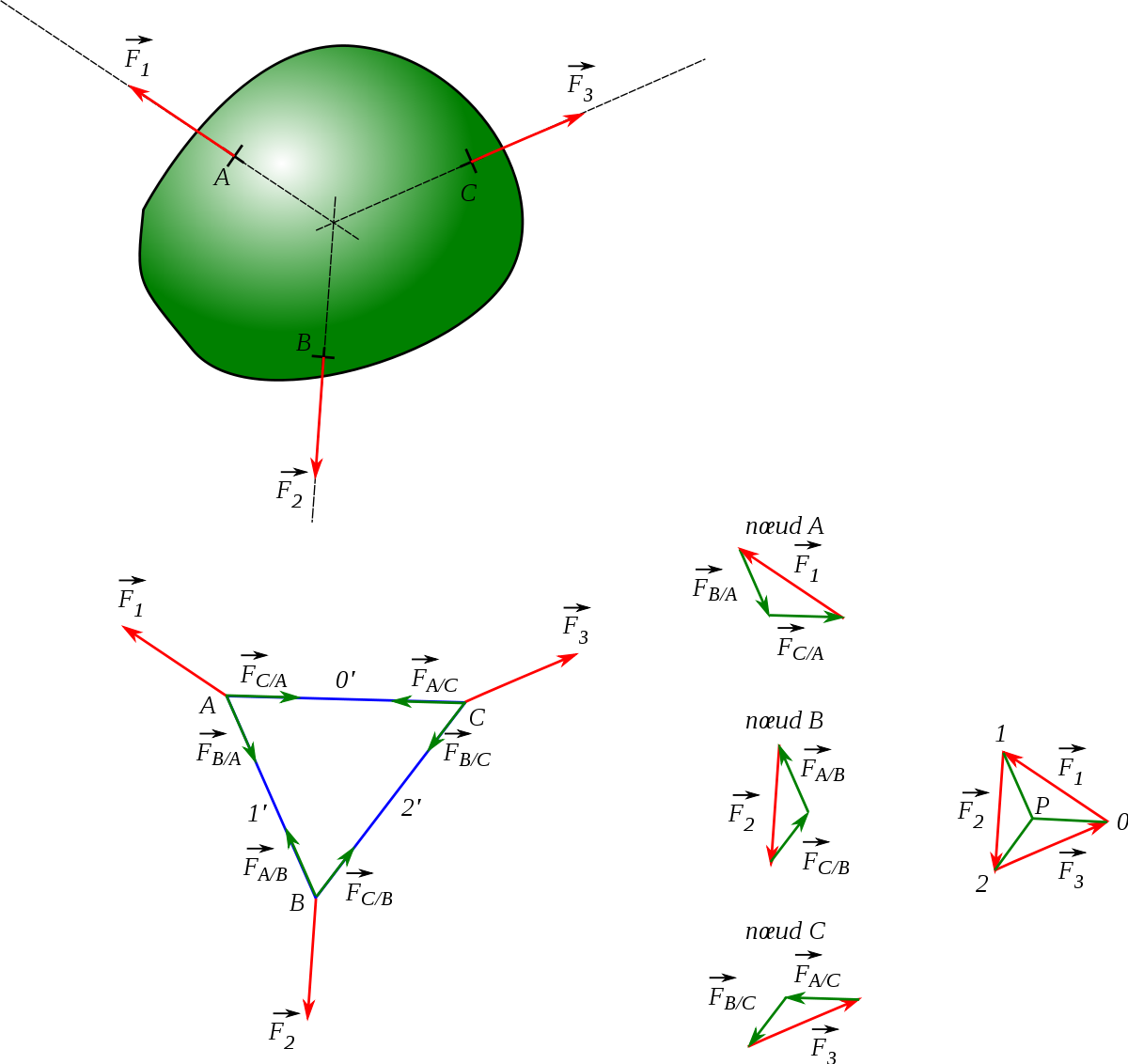
Le funiculaire consiste à remplacer l'objet étudié par un treillis — une structure composée de poutres articulées (liaisons pivot) — qui est en équilibre sous l'action des mêmes forces. Les segments joignant le pôle aux angles du dynamique sont les forces qui s'exercent dans ces poutres (traction ou compression).

Flexion des poutres

Étude de la flexion d'un ballon de reflux sous l'effet du poids : modélisation

Utilisation du funiculaire pour déterminer le diagramme des moments fléchissants ; la charge répartie q est remplacée par des charges ponctuelles, le polygone ainsi formé donne une approximation de la courbe

Utilisation du funiculaire pour déterminer la déformée : les moments fléchissants sont considérés comme une charge répartie, le funiculaire donne la déformée, si l'on choisit bien la position du pôle

Comparaison des résultats obtenus graphiquement (en cyan) avec la méthode des éléments finis (en rouge).

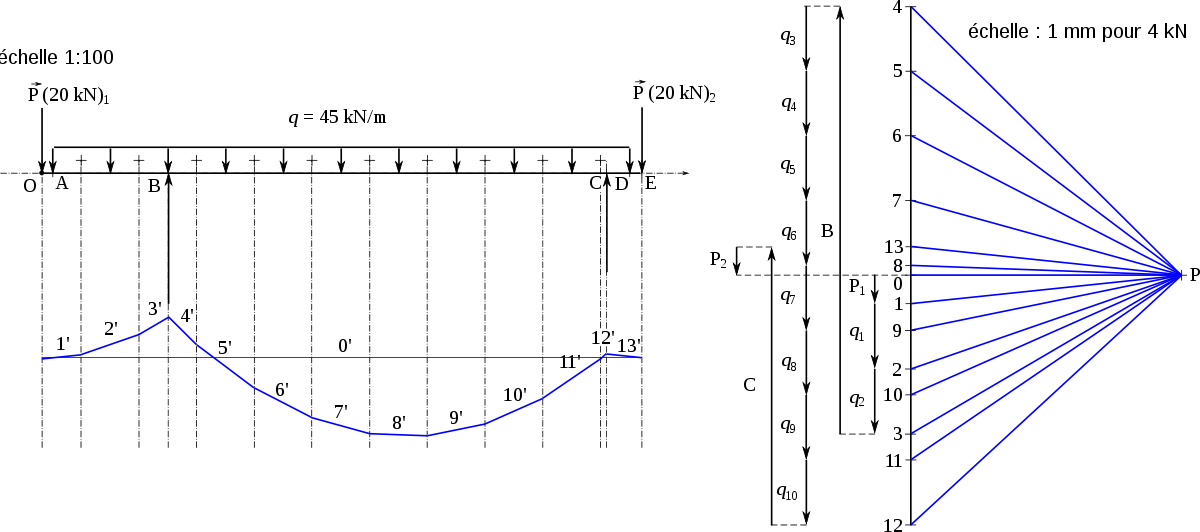
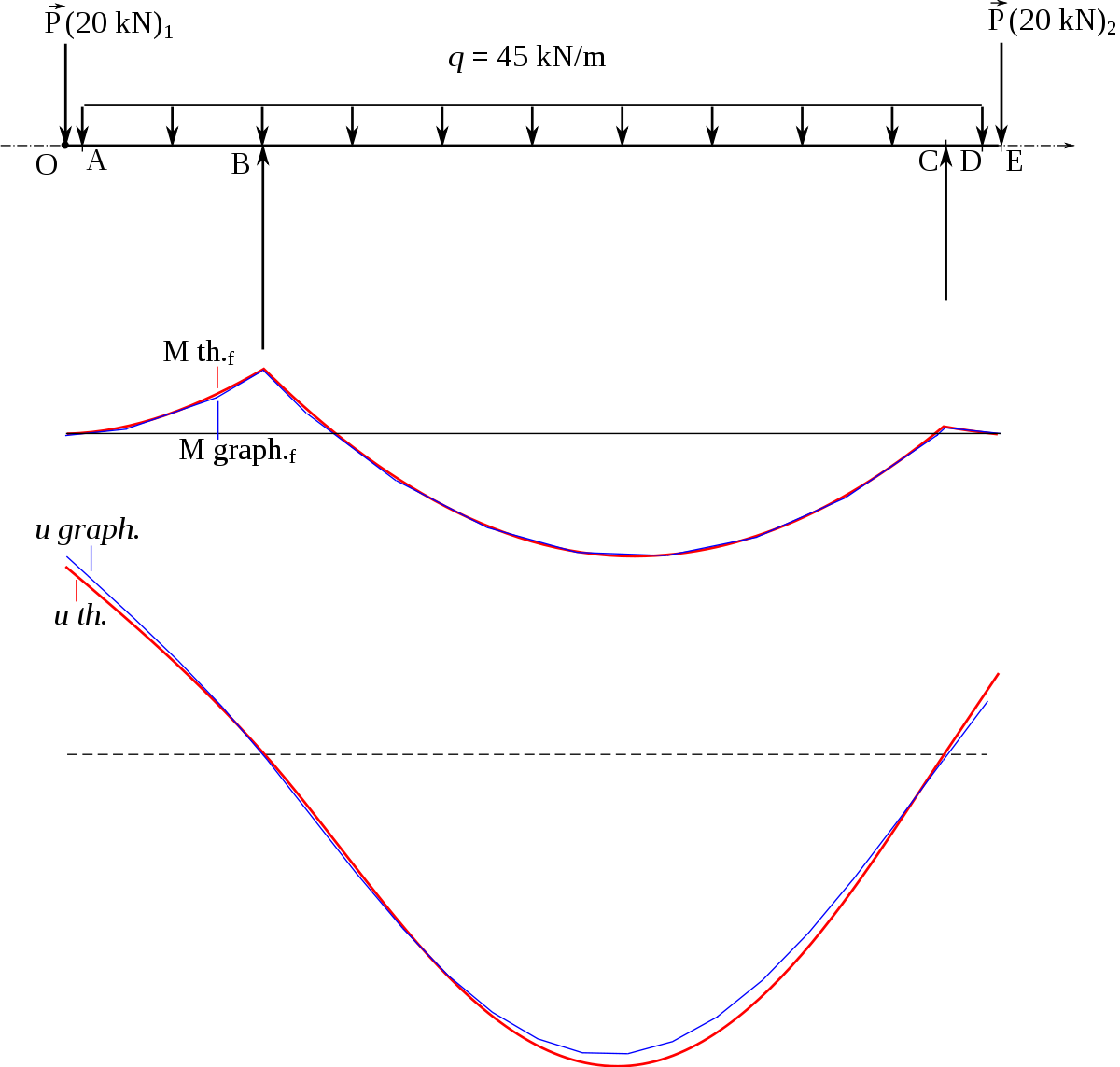
Le funiculaire est un moyen de faire une intégration graphique. On peut ainsi déterminer le diagramme des moments fléchissants ainsi que la déformée ; la détermination graphique de la déformée est appelée méthode de Mohr.

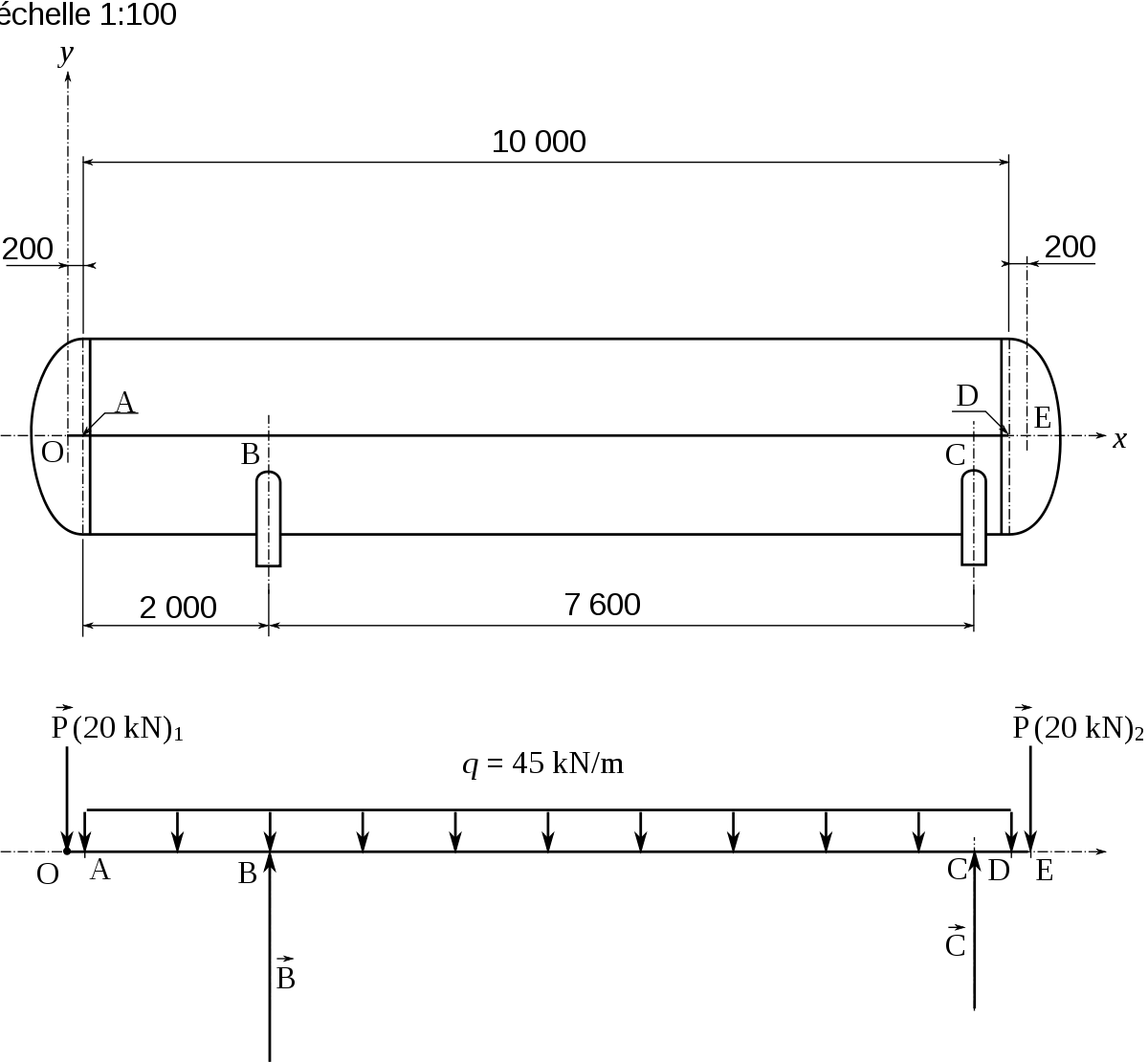
Le dynamique étant fait, on déplace le pôle pour que la ligne joignant les forces extrêmes soit horizontale. Le coefficient directeur des droites polaires est ainsi proportionnel aux intensités des forces cumulées. Le funiculaire que l'on trace présente des segments de droite y = ƒ(x ) où y est proportionnel à l'intensité de la force (pente de la droite) et à l'éloignement x, y représente donc un moment. Le funiculaire forme en fait le diagramme des moments fléchissants M_f, à l'échelle près. Cette échelle est déterminée par l'échelle des longueurs a (1 mm sur le dessin représente a mm réels soit 1:a), l'échelle des forces b (1 mm sur le dessin représente b N soit b N/mm) et la distance polaire p (distance du point P à la droite des forces) : 1 mm sur le diagramme des moments fléchissants représente abp Nmm.

Si l'on place le pôle à droite, on est en convention des efforts à droite de la coupure.

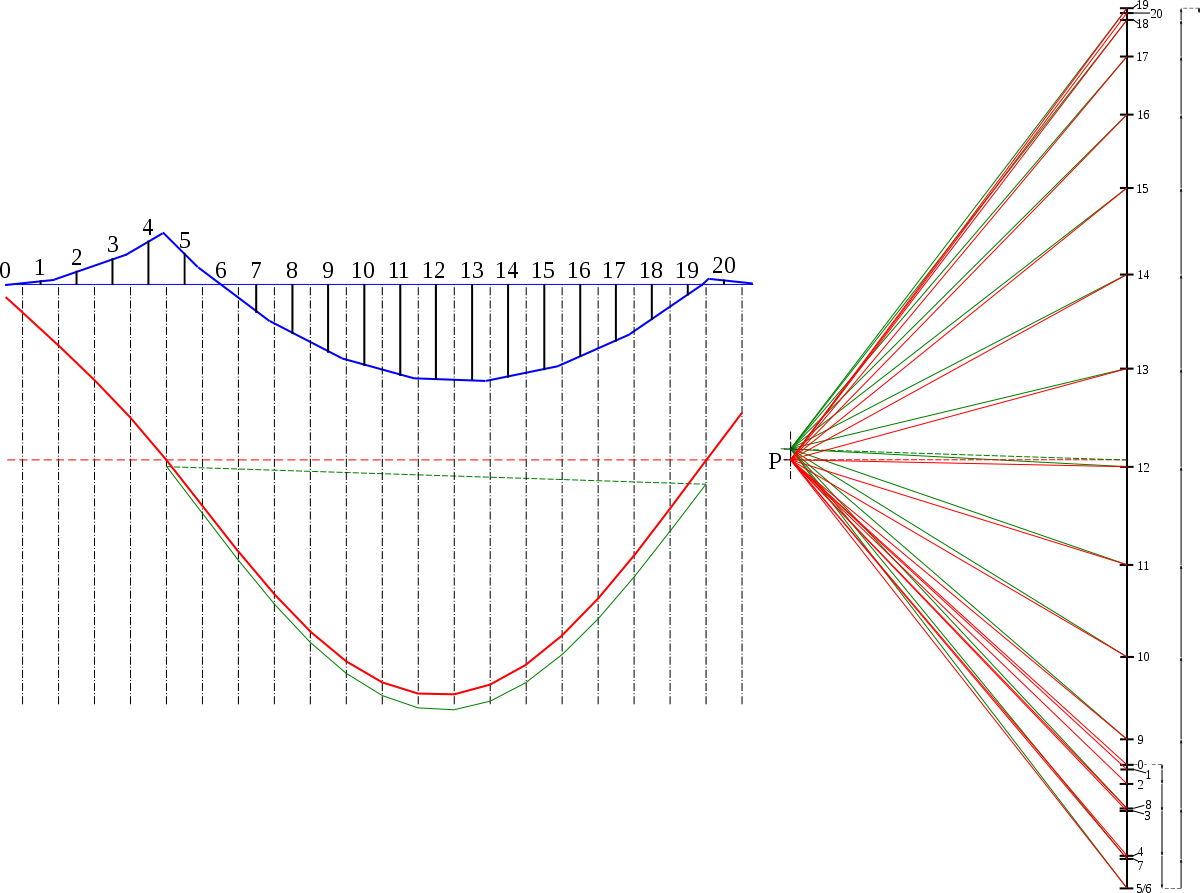
Si l'on découpe le diagramme des moments fléchissants en bandes d'égale largeur, l'aire de ces bandes est une primitive de la fonction. En considérant que ces aires sont des poids, appelé « charge fictive », et en traçant le funiculaire, on fait une intégrale graphique double, ce qui donne le profil de la déformée u(x ). À un facteur près, la largeur réelle H des trapèzes, l'aire est égale à l'ordonnée au milieu du segment. La charge fictive est en fait M_f/(EI_Gz), E étant le module de Young du matériau et I_Gz le moment quadratique de la section droite par rapport à l'axe de flexion z ; si h est la largeur des trapèzes, l'échelle des charges fictive est donc 1 mm pour ha²bp/(EI_Gz) mm^-1.

Le pôle doit être placé à gauche ; cela correspond au fait qu'il y a un signe moins dans l'équation de la déformée lorsque l'on est en convention des efforts à droite de la coupure (M_f = -EI_Gzu"), et un signe plus lorsque l'on est en convention des efforts à gauche de la coupure (M_f = EI_Gzu"). Si p’ est la distance polaire utilisée pour tracer la déformée, alors 1 mm sur la figure correspond à ha³bpp’/(EI_Gz) mm dans la réalité. Le choix de distances polaires p et p’ permet de simplifier le calcul de l'échelle.

Si la section droite varie, il faut alors tracer un diagramme des charges fictives M_f/(EI_Gz) prenant en compte les variations du moment quadratique avant de tracer le funiculaire.

La précision de la méthode dépend de la précision du tracé et du nombre de trapèzes utilisés pour découper les charges réparties et le diagramme des moments fléchissants. Pour un tracé précis, on réalise une épure au format A0. Les erreurs se cumulent, le tracé de la déformée est donc plus éloigné de la solution théorique que le diagramme des moments fléchissants.