Nombre cardinal - Définition

Hypothèse du continu

L'inégalité montrée ci-dessus permet d'écrire puisque est le plus petit cardinal strictement supérieur à .

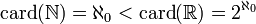
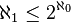
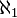
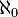
L'hypothèse du continu affirme l'égalité . On montre que cette propriété est indécidable dans ZFC. Par extension, l'hypothèse généralisée du continu énonce que, pour tout ordinal α, on a .

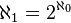
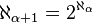
Les résultats suivants s'obtiennent en admettant comme axiome l'hypothèse généralisée du continu.

• Il y a équivalence entre les notions de cardinaux faiblement inaccessibles et fortement inaccessibles.
• En notant l'ensemble des fonctions de dans , il vient
  • si  ;
  • si  ;
  • si .

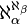
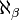
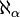
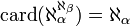
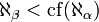
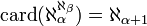
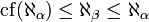
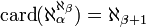
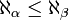
Une reformulation de l'hypothèse du continu est que R, l'ensemble des réels, est bien ordonnable de type ℵ₁. C'est un énoncé plus fort que le simple fait que R peut être bien ordonné, qui équivaut dans ZF à l'axiome du choix sur les sous-ensembles des réels.

Une forme forte de l'hypothèse généralisée du continu, énoncée pour des ensembles infinis quelconques, a pour conséquence l'axiome du choix (voir l'article Ordinal de Hartogs).