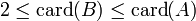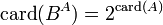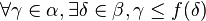Nombre cardinal - Définition
La liste des auteurs de cet article est disponible ici.
Cardinal fini
Le cardinal d'un ensemble fini correspond donc simplement au nombre d'éléments qu'il contient. Par exemple, card({1,2,5}) = 3.
Toute partie d'un ensemble fini est finie.
Propriétés générales
Si f est une fonction de A dans B, alors
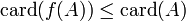
Théorème fondamental
Il n'existe pas de surjection d'un ensemble E sur l'ensemble de ses parties
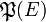
-
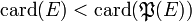
C'est le théorème de Cantor.
Ce résultat justifie le fait qu'il existe différents nombres cardinaux infinis. Il donne même un procédé de construction d'une infinité d'entre eux par itération de la fonction ensemble des parties.
Les cardinaux infinis sont représentés au moyen de la lettre hébraïque aleph
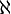
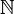
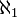
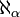
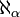
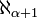
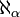
Cardinal inaccessible
L'accessibilité est la possibilité d'atteindre un ordinal ou un cardinal donné à partir des ordinaux plus petits.
Un ordinal α est dit cofinal avec un ordinal β inférieur s'il existe une application strictement croissante f de β dans α tel que α soit la limite de f au sens suivant :
Par exemple,
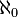
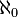
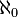
Par contre, le cardinal
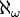
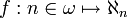
Ce cardinal
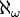
En notant cf(α) le plus petit ordinal pour lequel α est cofinal, on obtient
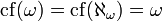
Les cardinaux se classent alors comme suit :
- ceux de la forme
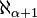
- ceux de la forme
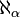
- ceux de la forme
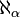
Ce dernier type de cardinal est qualifié de faiblement inaccessibles car ils ne peuvent être construits à partir de cardinaux plus petits. On distingue parmi eux les cardinaux fortement inaccessibles qui vérifient de plus
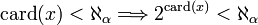
Les deux premiers types de cardinaux sont qualifiés au contraire d'accessibles, car on peut les construire (dans ZFC) à partir de cardinaux plus petits qu'eux.
Cardinal infini
Si A est infini alors
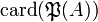
Exemples
- Le cardinal de l'ensemble des nombres réels est le même que celui de l'ensemble des parties de
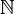
-
 .
.
- Ce cardinal étant égal à celui de


- Cependant, l'ensemble des entiers naturels et l'ensemble des rationnels sont équipotents.
-
-
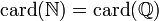
-
- De même que
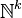
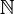
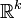
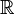
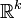

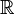
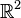
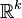
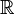

- Le cardinal de l'ensemble des fonctions continues de




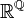
- Le cardinal de l'ensemble des fonctions de


 .
.
Propriétés
- Un ensemble A est infini si et seulement si
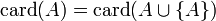
- Si A est infini et si
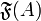
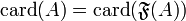
- Si A est infini et B non vide, alors
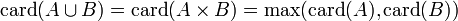
- Si B est inclus dans A infini avec card(B) < card(A), alors
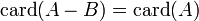
- Si A est infini, alors
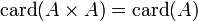
- Si A est infini et si