Nombre cardinal - Définition

Introduction

En mathématiques, les nombres cardinaux, ou simplement cardinaux, généralisent les nombres entiers naturels pour pouvoir « compter » les éléments d'un ensemble, même infini. On parle du cardinal d'un ensemble, qui, dans le cas des ensembles finis, est simplement son nombre d'éléments.

L'outil mathématique qui permet d'aborder la cardinalité est la bijection : deux ensembles ont même cardinal quand on peut les mettre en bijection, et on dit alors qu'ils sont équipotents. Cette caractérisation est conforme à l'intuition pour les ensembles finis, et se généralise de façon satisfaisante aux ensembles infinis. Le point de départ de la théorie de la cardinalité pour les ensembles infinis fut un article de 1874 de Georg Cantor qui montrait que le continu, l'ensemble des réels, ne pouvait être mis en bijection avec l'ensemble des entiers naturels, et que donc il existait des infinis différents du point de vue de la cardinalité.

Pour représenter un nombre cardinal en théorie des ensembles, on peut choisir un ensemble de référence parmi une classe d'ensembles équipotents entre eux. Ainsi on appelle dénombrable un ensemble équipotent à l'ensemble des entiers naturels. Pour un ensemble en bijection avec l'ensemble des réels, ont dit qu'il a la puissance du continu (puissance était utilisé dans le sens du cardinal, et a donné également équipotent). Une première théorie de la cardinalité peut se construire comme une théorie de la relation d'équipotence, sans définir ce qu'est vraiment un nombre cardinal en toute généralité.

Il existe plusieurs options pour définir la notion de nombre cardinal en toute généralité. Dans la théorie des ensembles ZFC (Zermelo-Fraenkel avec axiome du choix) et ses extensions, on utilise une généralisation à l'infini des nombres entiers en tant qu'ils permettent de numéroter dans un certain ordre, les nombres ordinaux, dont la représentation en théorie des ensembles est due à von Neumann. Dans ce cadre, un nombre cardinal est alors défini comme un nombre ordinal (de von Neumann) qui n'est équipotent à aucun ordinal qui lui soit strictement inférieur. Tous les entiers naturels, qui sont aussi des ordinaux finis, sont des cardinaux en ce sens. Les autres cardinaux, qui sont les cardinaux infinis, sont énumérés par la suite ordinale des alephs, mais on ne peut pas placer précisément la puissance du continu sur cette échelle dans le seul cadre de la théorie ZFC : c'est l'indépendance de l'hypothèse du continu.

En théorie des ensembles, les « grands cardinaux » permettent une extension naturelle de la théorie ZFC. L'étude de la cardinalité en théorie des ensembles est toujours un sujet de recherche actif.

Le concept

Les saisons, les points cardinaux, les fils Aymon, forment trois ensembles partageant une certaine qualité, qu'ils ne partagent pas avec l'ensemble des doigts de la main : on peut mettre en évidence cette qualité en faisant correspondre un à un les éléments respectifs de ces ensembles et dire qu'ils sont de cardinal « quatre ». « Quatre » serait alors la signature de la propriété en question.

De la même façon l'ensemble des doigts de la main peut être mis en correspondance, élément par élément, avec l'ensemble des mots {« Amérique », « Afrique », « Antarctique », « Océanie », « Eurasie »} ; ces deux ensembles sont en un certain sens équivalents.

Cependant, il n' y a aucun moyen de mettre en correspondance « un à un » chaque point cardinal avec chaque doigt de la main; et donc là on n'a pas affaire à des ensembles équivalents.

Ce que l'on appelle « cardinal » sera en quelque sorte la mesure de la « puissance » d'un ensemble.

Ainsi donc, tant qu'on en reste au fini, les cardinaux apparaissent sous le double aspect de l' équivalence et de l' ordre : chacun d'eux est la signature d'une équivalence entre ensembles, mais entre eux ils sont ordonnés par taille.

On verra plus bas que la situation se complique lorsque l'on a affaire à des cardinaux infinis, ainsi l'affirmation que de deux cardinaux l'un doit être supérieur à l'autre, dépend de l'axiomatique choisie : c'est le problème de la comparabilité cardinale.

Définition de Frege

La relation d'équipotence étant réflexive, symétrique et transitive sur la classe des ensembles, chaque classe d'équivalence est appelée nombre cardinal ou simplement cardinal.

Cette définition qui paraît très naturelle se présente parfois dans les exposés élémentaires de la théorie des ensembles ; cependant son usage pose certains problèmes dans les théories usuelles, ainsi la classe des ensembles à un seul élément, qui serait le nombre "un", n'est pas un ensemble et n'est élément d'aucune classe ; de même la classe des ensembles à quatre éléments, etc, d'où l'impossibilité de même parler d'intervalles de nombres entiers naturels. Ces difficultés s'apparentent au paradoxe de Russell, qui fut d'ailleurs découvert quand ce dernier adressa une lettre critique à Frege.

Définition classique

Dans la théorie des ensembles de Zermelo-Fraenkel (ZF), l'adjonction de l'axiome du choix (donnant la théorie ZFC) permet de définir le cardinal d'un ensemble comme le plus petit nombre ordinal qui lui est équipotent. Un nombre cardinal est alors un ordinal qui n'est équipotent à aucun de ses éléments.

S'il existe une injection d'un ensemble A dans un ensemble B alors il existe une injection de n'importe quel ensemble équipotent à A dans n'importe quel ensemble équipotent à B. Le théorème de Cantor-Bernstein permet de montrer que deux cardinaux sont égaux s'il existe une injection de chacun d'eux dans l'autre. Cette relation est donc une relation d'ordre (partiel) sur les cardinaux. L'affirmation que l'ordre est total équivaut à l'axiome du choix.

L'ensemble vide et les ensembles d'entiers de la forme forment des ensembles de cardinaux deux à deux différents.
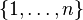
Un ensemble est dit fini s'il est équipotent à l'un de ces ensembles, infini dans le cas contraire. Tout cardinal fini est inférieur à tout cardinal infini.

Sans l'axiome du choix, on ne peut associer un tel cardinal qu'aux ensembles qui peuvent être munis d'un bon ordre.

On note et , de sorte que l'ordre sur les cardinaux prolonge l'ordre sur les entiers naturels.

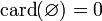
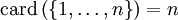
L'ensemble vide est le seul ensemble à n'être équipotent qu'à lui-même.

Avec la définition des entiers de Von Neumann, qui est le cas particulier restreint au fini de la définition des ordinaux, un entier naturel n est l'ensemble de ses prédécesseurs , en particulier .

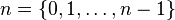
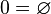
La suite ordinale des alephs énumère tous les nombres cardinaux (en ce sens) infinis.