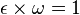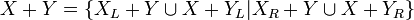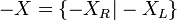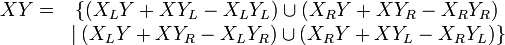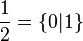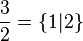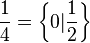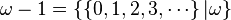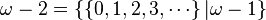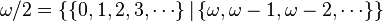Nombre surréel et pseudo-réel - Définition

Introduction

En mathématiques, les nombres surréels sont un corps qui inclut tous les nombres réels, ainsi que tous les ordinaux transfinis et leurs inverses, respectivement plus grands et plus petits que n'importe quel nombre réel positif.

Les nombres surréels ont été introduits par John Conway et popularisés par Donald Knuth en 1974 dans son livre Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness (Les nombres surréels : comment deux ex-étudiants se mirent aux mathématiques pures et trouvèrent le bonheur total).

Les nombres pseudo-réels, également introduits par Knuth, sont un sur-ensemble des nombres surréels, construit avec des conditions plus faibles que ces derniers.

Nombres surréels

Présentation

La construction des nombres surréels est similaire à la construction des nombres réels via les coupures de Dedekind, mais utilise le concept de récurrence transfinie. Elle repose sur la construction de nouveaux nombres représentés grâce à deux ensembles de nombres déjà construits, L et R (pour left et right, gauche et droite), éventuellement vides. Le nouveau nombre ainsi construit, noté , sera plus grand que tout nombre de L et plus petit que tout nombre de R, selon un ordre qui sera défini plus loin. Pour que cela soit possible, on impose une restriction sur L et R : il faut que chaque nombre de L soit plus petit que chaque nombre de R.

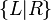
Définition

Soient L et R deux ensembles de nombres surréels tels que :

• pour tout et tout ,
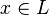
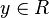
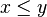
• L et R sont bien fondés

Alors, est un nombre surréel.

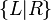
Étant donné un nombre surréel , on appelle X_L et X_R l'ensemble de gauche et l'ensemble de droite de X, respectivement.

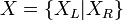
Pour éviter l'inflation d'accolades, on abrégera en , en et en .

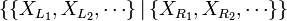
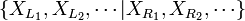
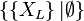
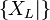
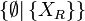
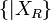
On constate qu'il s'agit d'une définition récurrente ; ce point sera explicité plus tard.

Ordre

Pour que la définition ci-dessus ait un sens, il est nécessaire de définir une relation binaire (notée ≤) sur les nombres surréels.

Soient deux nombres surréels et . si et seulement si pour tout , on ne rencontre jamais et si pour tout , on n'a jamais .

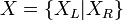
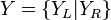
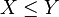
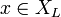
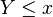
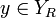
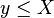
Là encore, cette définition est récurrente.

Cette relation ne définit qu'un pré-ordre car elle n'est pas antisymétrique (on peut avoir et sans que X = Y, c'est le cas par exemple avec et ). Pour contourner ce problème, on définit une nouvelle relation sur les nombres surréels :

.

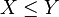
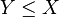
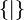
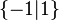
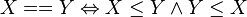
Il s'agit d'une relation d'équivalence et l'ordre induit par sur les classes d'équivalences est un ordre total, une classe d'équivalence pouvant alors être considérée comme un nombre unique.

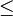
Opérations

• On définit l'addition de deux nombres surréels par :

avec et .

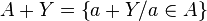
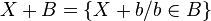
• La négation :

avec .

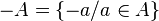
• Quant à la multiplication de deux nombres surréels :

avec .

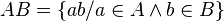
Il est possible de montrer que ces opérations sont bien définies sur les nombres surréels. On peut les généraliser sans ambiguïté aux classes d'équivalence définie plus haut par :

• Si [X] = [X'] et [Y] = [Y'], alors [X + Y] = [X' + Y'],
• [ − X] = [ − X'] et
• [XY] = [X'Y'].

Finalement, on peut montrer que ces opérations sur les classes d'équivalence définissent un corps ordonné, avec la mention qu'elles ne forment pas un ensemble, mais une classe propre. Il est possible de montrer qu'il s'agit du plus grand corps ordonné, c'est-à-dire que tout corps ordonné peut y être plongé.

À partir de maintenant, on ne fera plus la distinction entre un nombre surréel et sa classe d'équivalence et on appellera directement cette dernière nombre surréel.

Construction

On l'a vu, les deux définitions précédentes utilisent le principe de récurrence. Il est possible d'utiliser la récurrence ordinaire, mais il est plus intéressant de prendre en compte la récurrence transfinie.

Il est également nécessaire de créer un nombre surréel afin d'initier la récurrence ; peut être défini grâce à l'ensemble vide et répond à cette fonction.

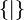
Désignons par N_n, pour un ordinal n, l'ensemble des nombres surréels créés à l'étape n de la récurrence, en prenant . On appelle date de naissance d'un nombre surréel X le plus petit ordinal n tel que .

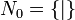
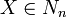
Les nombres surréels créés en un nombre fini d'étapes (par un raisonnement de récurrence ordinaire, donc) sont assimilés aux rationnels dyadiques (c'est-à-dire les nombres p / 2ⁿ où p et n sont entiers).

Exemples

On définit de proche en proche :

• Les entiers :

et

et

.

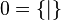
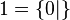
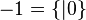
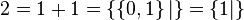
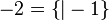
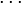
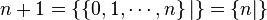
• Les nombres dyadiques :

• Les autres nombres rationnels, comme coupures entre deux ensembles de nombres dyadiques, de la même façon que les nombres irrationnels sont définis comme coupures entre rationnels.

• Les infiniments grands :

qui est plus grand que n'importe quel nombre entier

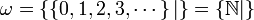
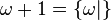
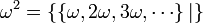
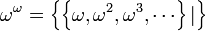
Mais aussi de nouveaux objets qui ne sont pas des ordinaux, comme

• Les infiniments petits :

qui est strictement positif mais inférieur à tout , pour n entier positif.

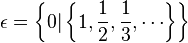
On peut montrer que .