Oméga de Chaitin - Définition

Importance du nombre Omega dans la Théorie algorithmique de l'information

Pourquoi ce nombre est-il défini ainsi ? Pourquoi est-il si important ?

Un des grands succès de la théorie algorithmique de l'information est d'avoir permis la définition rigoureuse de la notion de nombre aléatoire, ou de suite aléatoire. Selon cette théorie, un nombre est aléatoire si et seulement s'il n'existe pas d'algorithme plus petit que la taille même du nombre pour le générer. Pour poursuivre ce succès et exercer la théorie, l'étape naturelle suivante était de se demander s'il était possible d'exhiber et donner un exemple de nombre aléatoire ainsi défini.

Paradoxalement, bien qu'un nombre réel sélectionné au hasard soit aléatoire avec une probabilité de 1 (c'est à dire que quasiment tous les nombres réels sont aléatoires), il est excessivement difficile d'en exhiber, ou d'en décrire, un.

En effet, pour exhiber un nombre, il faut soit le nommer ou le décrire d'une manière cohérente, et montrer que le nombre ainsi désigné "existe", possède un sens, ce qui n'est absolument pas évident a priori notamment a cause du paradoxe de Berry, et n'est pas ambigu (désigne un et un seul nombre). Ou alors, il faut donner un algorithme pour le construire et le générer, mais cela est par définition impossible pour un nombre aléatoire. Enfin, et surtout, il faut prouver que le nombre décrit est bien aléatoire.

Il est encore plus difficile d'exhiber un tel nombre qui possède une signification et des propriétés mathématiques précises, sans être une simple suite de chiffres aléatoires sans signification.

Le nombre Omega franchit toutes ces difficultés, et est l'exemple le plus emblématique de nombre incompressible, aléatoire, qui peut être désigné sans ambiguïté, et possède un sens et des propriété profondes et intéressantes. A ce titre, il constitue un des éléments très important de la théorie algorithmique de l'information.

Démonstration formelle de la formule

Les programmes auto-délimités

La définition d'une probabilité d'arrêt suppose qu'aucun programme ne résulte de l'extension d'un autre.

On considère une fonction F à deux arguments. F est dite universelle si pour toute fonction calculable f d'une seule variable x il y a une constante p telle que pour tout x, F(p,x) = f(x) ; en d'autres mots, F peut être utilisée pour simuler n'importe quelle fonction calculable d'une seule variable. p représente un "programme" pour f, et F représente un émulateur qui exécute ce programme ; pour chaque p, f(x) = F(p,x) est calculable.

Le domaine de F est l'ensemble de tous les programmes p tels que F(p,x) soit définie pour au moins une valeur de x. Selon la convention ci-dessus, il n'existe pas dans le domaine deux programmes différents p₁ et p₂ tels que l'un d'eux soit une extension de l'autre : on dit que F est sans préfixe.

Ceci revient à parler de la machine universelle (machine de Turing) correspondant à F dont les programmes ont une séquence de fin.

Interprétation comme probabilité

On considère l'espace de Cantor formé de toutes les suites infinies de 0 et de 1. Une probabilité d'arrêt peut être interprétée comme la mesure d'un certain sous-ensemble de cet espace.

La mesure probabiliste dans cet espace est définie de façon à ce que pour toute chaîne x l'ensemble des suites qui commencent par x mesure 2^-|x|. Ceci entraîne que pour tout entier naturel n l'ensemble des suites f de l'espace de Cantor telles que f(n) = 1 mesure 0,5 et que l'ensemble des suites dont le n^ième élément est 0 mesure aussi 0,5.

Soit une fonction universelle calculable sans préfixe telle que décrite plus haut. Le domaine de est un ensemble infini de chaînes :

.

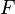
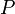
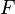
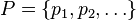
Chaque détermine un sous-ensemble S_i de l'espace de Cantor, ce sous-ensemble contient toutes les suites qui commencent par . Les S_i étant disjoints - puisque par hypothèse aucun des n'est inclus dans un autre - la somme :

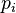
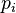
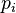
représente la mesure de .

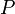
De cette façon, Ω_F est la probabilité qu'une suite de l'espace de Cantor choisie au hasard commence par une chaîne qui soit un élément du domaine de . C'est pour cette raison que Ω_F s'appelle la "probabilité" d'arrêt.