Oméga de Chaitin - Définition

Enjeux et propriétés du nombre Oméga

Preuves de problèmes non résolus en mathématiques par un nombre Oméga

La connaissance d'un Oméga de Chaitin permettrait, en théorie, de résoudre certains problèmes en théorie des nombres, dont certains non résolus à ce jour comme la conjecture de Goldbach et l'hypothèse de Riemann.

Par exemple, la conjecture de Goldbach affirme que tout nombre pair plus grand que 2 est la somme de deux nombres premiers. Pour prouver cette conjecture à l'aide d'un nombre Oméga, il s'agirait de réaliser un programme qui recherche la décomposition de tous les nombres pairs en somme de deux nombres premiers. Pour un nombre pair donné, il est possible pour un programme de déterminer si la conjecture est vraie ou fausse en un temps fini (soit en trouvant la somme, soit en épuisant toutes les possibilités sans en trouver, ce qui serait un contre-exemple à la conjecture). Si le programme trouve un contre-exemple, il s'arrête, sinon il continue de chercher un contre-exemple à l'infini.

Donc : si la conjecture de Goldbach est vraie, le programme ne s'arrête pas, si elle est fausse, le programme s'arrête (en retournant un contre-exemple).

En sachant si ce programme se termine ou non en utilisant le nombre Oméga, on pourrait donc savoir avec certitude que la conjecture est vraie ou fausse.

Cependant, tout cela reste théorique. En pratique, la méthode pour restituer les machines qui s'arrêtent à partir d'un nombre Oméga (autrement dit, pour "décompresser" un nombre Oméga, voir ) est si longue qu'elle est inapplicable en pratique. En effet, il est nécessaire d'attendre que tous les programmes qui doivent s'arrêter s'arrêtent avant de connaitre le statut de chaque programme. Comme il existe jusqu'à 2^N programmes de longueur N bits, et qu'un programme individuel peut théoriquement s'arrêter au terme d'un temps arbitrairement long, et que l'ordre de grandeur de N pour les problèmes mathématiques intéressants est de l'ordre du millier, il serait nécessaire d'attendre l'arrêt de jusqu'à programmes. Même si la moyenne des temps des programmes qui s'arrêtent est de l'ordre de la nanoseconde (ce qui est déjà en soi inenvisageable), l'âge de l'univers n'y suffirait pas.

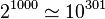
Calculabilité d'un nombre Oméga

Un nombre Oméga n'est pas calculable, car il est aléatoire : aucun algorithme qui ne contient pas déjà le nombre en lui-même ne peut donner de manière certaine et dans un temps fini les N premiers bits d'un nombre Oméga. Cependant, le statut de ces nombres vis à vis de la calculabilité n'est pas trivial et mérite quelques précisions.

Un nombre Oméga n'est pas un nombre calculable, mais est un nombre approchable. Cela signifie qu'il existe une séquence calculable et jamais décroissante de rationnels qui converge vers ce nombre. C'est précisément cette caractéristique qui est mise en oeuvre dans la , pour calculer une approximation de plus en plus précise d'un nombre Oméga (puisque on "stoppe" la décompression quand l'approximation égale le nombre Oméga).

Le problème est que cette séquence est convergente, mais on n'a aucun moyen de savoir (cela est non calculable) quels bits ou même combien de bits seront exacts au terme de combien de temps. De plus, il a été démontré que la convergence vers un nombre Oméga par une séquence approchante est plus lente que n'importe quelle autre séquence convergente calculable. Même si une séquence approchante calculable existe, elle ne peut donc être utilisée pour calculer en pratique, et même en théorie, un nombre Oméga, qui reste de ce fait bel et bien non-calculable.

Il peut paraître dès lors paradoxal de constater que la valeur exacte des N premier bits de nombres Oméga ont été déterminés pour certaines machines de Turing universelles. Mais cela ne contredit pas les résultats précédents, pour la raison suivante : la détermination de ces bits utilise un mélange de calcul et de raisonnements mathématiques, pour prouver que certains programmes ne s'arrêtent pas ou ne peuvent contribuer significativement à la somme finale. Le raisonnement mathématique étant une sorte de calcul, cette constatation ne semble pas faire avancer le paradoxe. Seulement, il a été prouvé qu'un système formel mathématique (utilisé pour les raisonnements mathématiques, comme ZFC par exemple) fondé sur des axiomes qui représentent N bits d'information, ne pourra jamais déterminer plus de N+O(1) bits d'un nombre Oméga par des raisonnements mathématiques (le nombre exact de bits que peut déterminer la théorie est incalculable). On peut donc déterminer un certain nombre de bits d'un nombre Oméga, mais un nombre fini, incalculable, et d'autant plus faible que le système formel utilisé pour les raisonnements est élégant, et fondé sur un nombre le plus petit possible d'axiomes.

Nombre Oméga et l'incomplétude des mathématiques

Un nombre Oméga pose un défi à toute théorie, à tout système formel, mathématique. Chaque bit d'un nombre Oméga représente, indépendamment des problèmes plus profonds qu'il peut résoudre, un théorème mathématique simple :

Chacun de ces théorèmes est soit vrai soit faux dans l'absolu. Le Nième bit possède une valeur déterminée et univoque, même si elle ne peut pas être calculée : les machines de Turing qui contribuent à la détermination de ce bit s'arrêtent ou bien ne s'arrêtent pas dans l'absolu.

De plus, un nombre Oméga étant incompressible, l'infinité des théorèmes "Oméga N" sont autant de problèmes indépendants à résoudre pour une théorie mathématique. La complexité des mathématiques pures est infinie.

En 1931, Kurt Gödel a démontré l'incomplétude des théories mathématiques par le fameux théorème d'incomplétude de Gödel : il existe dans toute théorie mathématique suffisamment puissante, des énoncés qui ne sont pas démontrables et dont la négation n'est pas non plus démontrable. Ce sont des énoncés dit indécidables.

Les nombres Oméga apportent un éclairage complémentaire au théorème d'incomplétude de Gödel. Si on ne fait pas appel à la théorie algorithmique de l'information, la portée du théorème de Gödel n'est pas claire : Combien de théorèmes sont indécidables ? Est-ce l'exception ou la règle ? Les théorèmes indécidables se limitent-ils aux théorèmes "diagonaux" incontournables, ou sont-ils beaucoup plus répandus ? Est-il nécessaire d'augmenter le nombre d'axiomes pour diminuer le nombre de problèmes indécidables ? Quelle est la relation entre le nombre d'axiomes et le nombre de théorèmes indécidables ?

La théorie algorithmique de l'information et les nombres Oméga apportent des éléments de réponse à ces questions. En effet, selon la théorie algorithmique de l'information :

1. Le nombre de problèmes (de théorèmes) indépendants (qui ne dérivent pas les uns des autres) à résoudre par les théories mathématiques est infini (il y a, au moins, les théorèmes "Oméga N"). Pratiquement tous les théorèmes "Oméga N" sont indécidables pour un système formel type ZFC.
2. La complexité des théorèmes résolus par une théorie mathématique est limité par la complexité de l'ensemble de ses axiomes. Il s'agit du théorème d'incomplétude de Chaitin.
3. Donc le seul moyen de diminuer le nombre de problèmes indécidables est d'augmenter le nombre d'axiomes. Le nombre d'axiomes nécessaires pour résoudre les théorèmes "Oméga N" tend vers l'infini.

Selon ce point de vue, le théorème de Gödel a un impact très important sur la complétude des mathématiques : de très nombreux théorèmes, quasiment tous, sont indécidables. Les théorèmes vrais et démontrables sont un ensemble rare parmi l'ensemble des théorèmes vrais.

Mais on ne sait pas si des théorèmes "intéressants" des mathématiques ont une grande complexité (dans ce cas, ils seraient hors d'atteinte d'un système formel ayant trop peu d'axiomes), ou une complexité en définitive faible, ce qui est tout à fait possible. De plus, on pourrait arguer du fait que les théorèmes "Oméga N" sont des théorèmes artificiels, concernant un nombre spécialement construit pour être paradoxal, et ne sont pas représentatifs des véritables mathématiques.

Mais on peut démontrer qu'il existe une équation diophantienne A(n,x₁,x₂,...,x_m) = 0, associé à un nombre Oméga, telle qu'elle admet pour solutions un ensemble fini de m-uplets (x₁,x₂,...,x_m) si le théorème "Oméga n" est vrai, et un ensemble infini de m-uplets (x₁,x₂,...,x_m) si le théorème "Oméga n" est faux pour ce nombre Oméga.

En posant les choses de cette manière, les théorèmes "Oméga N" ne sont plus des théorèmes artificiels concernant un nombre étrange, mais d'authentiques problèmes mathématiques s'intéressant au nombre de solutions d'une équation.

Propriétés des nombres Ω

Les nombres Ω présentent maintes propriétés intéressantes et surprenantes.

• Un nombre Ω n'est pas calculable au sens de Turing : s'il l'était, on pourrait déterminer le problème de l'arrêt.
• Un nombre Ω est transcendant, puisqu'il n'est pas calculable, et son développement binaire, décimal ou dans n'importe quelle base, est donc infini.
• Le produit de deux nombres Ω est un autre nombre Ω (associé à une autre machine universelle), de même que la somme de deux nombres Ω si elle est strictement comprise entre 0 et 1, et toute suite calculable extraite des décimales d'un nombre Ω (comme une décimale sur deux, ou celles de rang premier) est un autre nombre Ω.
• Un nombre Ω est un nombre normal et un nombre univers en toute base : dans toute base de numération, ses décimales sont équiréparties, et toute suite finie de chiffres se trouve quelque part dans son expression dans cette base (dans tout nombre Ω écrit en binaire, il y a par exemple une suite d'un milliard de 0 successifs).
• Pour une théorie axiomatique récursivement axiomatisable qui permet d'interpréter l'arithmétique, par exemple l'arithmétique de Peano ou la théorie des ensembles, et sous une hypothèse de cohérence plus forte que la cohérence simple, il existe un rang à partir duquel, bien qu'un des énoncés "le bit suivant du développement binaire est 0" ou "le bit suivant du développement binaire est 1" (en binaire) soit vrai, il est impossible de démontrer lequel des deux l'est, c'est-à-dire qu'ils sont indécidables dans la théorie en question. Solovay a renforcé ce résultat, en modifiant astucieusement une fonction universelle de Chaitin, en fonction d'une théorie donnée (vérifiant les mêmes hypothèses), pour exhiber un nombre Ω, qui dépend donc de cette théorie, et dont il est impossible de décider un seul chiffre dans celle-ci.