Oméga de Chaitin - Définition

Introduction

Un nombre Oméga de Chaitin est une suite de bits représentant, sous forme concentrée, la solution du problème de l'arrêt pour tous les programme d'une machine de Turing universelle donnée.

En théorie algorithmique de l'information, une constante Oméga de Chaitin est un nombre réel défini comme étant la probabilité qu’un programme informatique auto-délimité, dont chaque bit est généré aléatoirement, finira par s'arrêter.

Ces programmes sont associé à une machine de Turing universelle, ou à un modèle de calcul donné. Il existe donc une infinité de constantes de Chaitin, chacune associée à un modèle de calcul.

Cette définition permet de caractériser de manière univoque et mathématiquement précise un nombre, qui possède la particularité d'être aléatoire et d'être non-calculable au sens de Turing : un algorithme donné ne permet de calculer qu'un nombre fini de ses décimales. Jusqu'à la définition de ce nombre, il n'existait pas d'exemple mathématiquement précis de nombre aléatoire pouvant être désigné autrement qu'en écrivant ce nombre aléatoire in-extenso.

Cette définition permet également de coder, sous la forme la plus compacte possible, la solution du problème de l'arrêt pour tous les programmes d'un modèle de calcul donné. Comme il est possible de traduire la plupart des problèmes mathématiques en terme de programme informatique qui s'arrête ou non, la connaissance d'un nombre Oméga permet - en principe - de démontrer un grand nombre de théorèmes ou de conjectures mathématiques, dont certains encore non résolus à ce jour comme l'hypothèse de Riemann.

Ce nombre apporte enfin un éclairage sur l'incomplétude des mathématiques, mis au jour par le célèbre théorème de Gödel, et d'apporter des éléments d'appréciation en ce qui concerne sa signification et sa portée.

Ces nombres ont été définis et étudiés par Gregory Chaitin.

Définition de la probabilité d'arrêt

Soit le domaine d'une machine de Turing universelle , c'est à dire l'ensemble des programmes p auto-délimités pouvant être exécutés par U qui s'arrêtent.

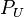
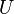
Alors :

,

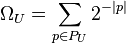
où | p | est la longueur de p.

Ce nombre est un nombre réel, compris entre 0 et 1, représentant la probabilité d'arrêt d'un programme dont les bits sont tirés aléatoirement, un par un, jusqu'à obtenir la séquence de bits définissant la limite du programme.

Origine, définition et construction du nombre Omega

Le "nombre de Borel"

Émile Borel s'est intéressé à la notion "d'accessibilité" et de définition d'un nombre. Selon Borel, pour qu'un nombre soit "bien spécifié", il faut d'une part que « deux mathématiciens, s’ils en parlent entre eux, soient certains qu’ils parlent du même nombre » et qu'il soit un « véritable "être" mathématique » qui doit « pour être intéressant aux yeux des mathématiciens, avoir au moins deux propriétés (en y comprenant celle au moyen de laquelle il a été défini) ». Il est effectivement très difficile pour un nombre purement aléatoire de posséder une autre propriété que sa propre méthode de construction.

D'autre part, Borel a imaginé en 1927 un nombre réel, le "nombre qui sait tout" (terminologie de G. Chaitin), résumant les réponses à toutes les questions formulables dans un langage donné, auxquelles on peut répondre par oui ou par non. Cette liste de questions constitue une liste infinie, mais dénombrable, que l'on peut trier alphabétiquement. On peut alors constituer un nombre, unique et bien spécifié, dont la Nième décimale binaire est la réponse à la Nième question.

Ces deux idées contiennent les germes du nombre Oméga. Chaitin, qui connait très bien l'œuvre de Borel, reconnait s'être inspiré de ces idées. Mais tout le travail de Chaitin va consister à transformer une idée mathématiquement inexploitable (car les questions et les réponses ne peuvent être mathématiquement formalisées), en un véritable "être mathématique", possédant de nombreuses propriétés démontrables, et deux caractéristiques a priori contradictoires : être "bien spécifié" et pourtant "inaccessible", non calculable et aléatoire.

Le "nombre de Turing"

Si on recycle l'idée du "nombre qui sait tout" pour définir un nombre dont la Nième décimale répond au problème de l'arrêt pour le Nième programme exécutable par une machine de Turing universelle, nous avons alors une définition précise d'un nombre et qui possède un sens mathématique, car le problème de l'arrêt est formalisé. De plus, étant donné que le problème de l'arrêt est non calculable, il s'ensuit que ce nombre est non calculable, ce qui est une condition absolument nécessaire (mais non suffisante) pour qu'il soit aléatoire. Enfin, injecter le problème de l'arrêt dans un nombre est susceptible de lui donner une importance fondamentale, car le problème de l'arrêt est au cœur de problèmes fondamentaux des mathématiques (ceux par exemple liés au dixième problème de Hilbert).

Tel quel, ce nombre n'est pas encore le nombre Omega, car il n'est pas aléatoire. En effet, ce nombre (que Chaitin nomme "Nombre de Turing" en hommage à l'inventeur du problème de l'arrêt), est hautement redondant et compressible. Or, une des définitions d'un nombre aléatoire est précisément d'être incompressible. Il faut donc trouver un moyen de compresser l'information contenue dans le nombre de Turing, et de la compresser au maximum possible.

Le nombre Omega

Représentation d'un ensemble de programmes auto-délimités sous forme d'un arbre binaire.
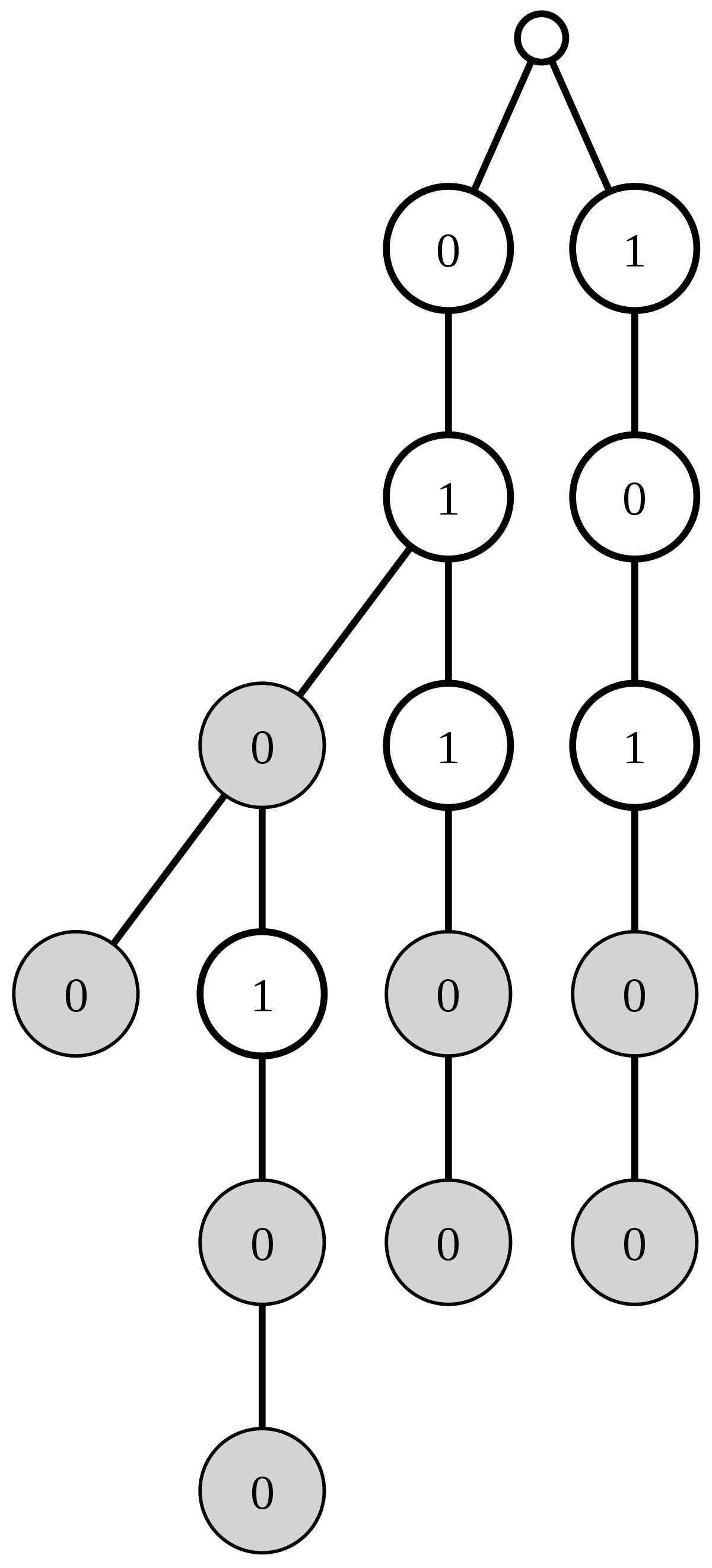
Ici, nous avons quatre programmes possibles, correspondant aux quatre "feuilles" de l'arbre : "01(00)", "011(00)", "0101(00)", et "101(00)"

Pour comprendre comment sera compressé le nombre Oméga, il est utile de voir pourquoi le nombre de Turing est hautement redondant. En fait, le nombre de Turing utilise N bits pour coder les résultats de N programmes, alors que Log2(N) bits sont suffisants. En effet, il suffit de connaitre le nombre de programmes de N bits qui s'arrêtent, sans savoir lesquels, pour déterminer les programmes qui s'arrêtent ou non.

Voici comment : si on connait le nombre P de programmes de N bits qui s'arrêtent, alors il suffit de générer tous les programmes de N bits, faire tourner ces 2^N programmes, et de s'arrêter quand P programmes seront arrêtés (ce qui arrivera certainement). On est alors sûr que les programmes restants ne s'arrêteront jamais. On connait donc les programmes qui s'arrêtent et ceux qui ne s'arrêtent pas. P est donc un nombre de au plus N bits codant les résultats du problème de l'arrêt pour 2^N programmes.

Le nombre Oméga va utiliser une idée similaire pour encoder ces informations de manière efficace et incompressible.

De la définition à la formule

Le nombre Omega est défini comme étant la probabilité qu'un programme, tiré aléatoirement, d'une machine de Turing universelle, s'arrête.

Le tirage aléatoire consiste à descendre aléatoirement dans l'arbre binaire représentant tous les programmes possibles pour une machine de Turing universelle U, jusqu'à tirer aléatoirement une séquence de fin, délimitant objectivement la fin de la représentation binaire du programme (voir figure ci-contre). En effet, la définition, et la formule, du nombre Oméga n'est valide que pour les programmes auto-délimités, c'est à dire contenant à leur fin une séquence de bits impossible à trouver dans le programme proprement dit. Le nombre de programmes de cette machine de Turing jusqu'à une profondeur N de l'arbre binaire (autrement dit, le nombre de programmes de longueur inférieure ou égale à N) est le nombre de feuilles de l'arbre.

Pour calculer la probabilité d'arrêt, il suffit à première vue de "compter" le nombre de programmes "feuille" qui s'arrêtent, et de diviser par le nombre total de feuilles, mais cela n'est vrai qu'à un niveau N donné. S'il existe un programme court dans l'arbre, on a beaucoup plus de chances de tomber aléatoirement sur lui qu'un programme long : il faut donc "pondérer" l'arrêt d'un programme p de taille |p| par 2 ^{− | p |} . Plus un programme est long, plus son poids est faible.

La formule du nombre Oméga en dérive directement; on additionne les poids pondérés de tous les programmes qui s'arrêtent :

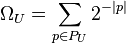
Cette somme converge et reste inférieure à 1, car les programmes sont auto-délimités : aucun programme n'est le prolongement d'un autre programme (en intégrant la séquence de fin). Par conséquent, un programme court va empêcher l'arbre de se développer après lui : on peut donc lui donner sans danger de divergence le "poids" de la partie de l'arbre qu'il a empêché de se développer, soit 2 ^{− | p |} . En donnant le "juste poids" à chaque nœud terminal, on démontre que l'on arrive au plus à la somme de "1" si on prend en compte tous les nœuds. Cette propriété est démontrée par les inégalités de Kraft.

Détermination de l'arrêt des programmes à partir du nombre Oméga

Mais le véritable but du nombre Oméga n'est pas de donner la probabilité d'arrêt d'un programme d'une machine de Turing donnée. Son but est de compresser sous la forme la plus compacte possible l'information d'arrêt de tous les programmes de cette machine de Turing. Il est donc nécessaire d'être en mesure de restituer ces informations à partir de la probabilité d'arrêt.

Soit Ω_n l'approximation d'un nombre Oméga consistant à prendre les N premiers bits de ce nombre Oméga. Comment, étant donné ce nombre Ω_n, déterminer les programmes de longueur inférieure à N bits qui s'arrêtent ou non ?

L'inégalité est évidente.

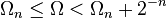
Si maintenant on génère tous les programmes possibles de taille inférieure ou égale à N bits, et si on les fait exécuter simultanément, on pourra calculer une approximation de plus en plus précise de Ω_n à chaque arrêt d'une machine, en ajoutant 2 ^{− l}, l étant la longueur du programme s'étant arrêté, à l'approximation précédente.

Dès que l'approximation de Ω_n atteint une valeur telle que l'ajout du poids d'un programme quelconque non encore terminé rendrait l'approximation supérieure ou égale à Ω_n + 2 ^{− n}, nous pouvons être certain que les programmes restants ne se termineront jamais. Les programmes de longueur inférieure ou égale à N qui ne s'arrêtent pas ont donc été identifiés dans un temps fini, à l'aide des N premier bits du nombre Oméga : Ω_n.

On établit au passage la propriété : les N premiers bits d'un nombre Oméga sont nécessaires et suffisants pour déterminer l'arrêt de tous les programmes de longueur inférieure à N bits.

Preuve que le nombre Oméga est incompressible, et donc aléatoire

Soit un nombre ω_n représentant le nombre le plus court possible permettant de déterminer le problème de l'arrêt pour tous les programmes jusqu'à une longueur de N bits.

Soit le programme COMPLEXE qui, en utilisant ce nombre, détermine la liste des machines de longueur inférieure ou égale à N bits, collectionne tous les résultats de ces machines, et retourne un nombre x n'appartenant pas à cette liste. Le programme COMPLEXE s'arrête.

Par définition, x ne peut être retourné par un programme de taille inférieure ou égale à N. COMPLEXE retournant ce nombre, il possède donc une taille supérieure à N. Comme COMPLEXE intègre ω_n dans son programme, il s'ensuit que TAILLE(COMPLEXE) = TAILLE(ω_n) + O(1) > N..

Le plus petit programme pour calculer les N premiers bits de Ω a une taille supérieure à N − O(1) , ce qui est la caractéristique d'un nombre aléatoire au sens de Levin-Chaitin. Oméga est donc bien incompressible et aléatoire.