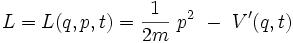Principe de moindre action et mécanique classique - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
- Introduction - Historique - Définition du lagrangien et de l'action classiques - Une alternative de présentation - L'équation fondamentale de la dynamique newtonienne - Équation d'Euler-Lagrange - Particule chargée dans un champ électromagnétique - Cas où il y a des forces de frottements - Invariances et constantes du mouvement - L'impulsion
L'impulsion
L'impulsion est la variable conjuguée de la vitesse dans la transformée de Legendre du lagrangien.
Elle est définie par :
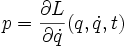
- Si
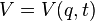
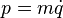
- Donc
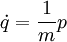
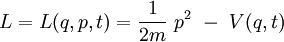
- Si
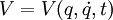
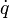
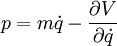
-
- où
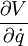
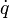
- où
- L'impulsion est utilisable comme variable :
- En remarquant que:
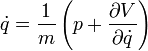
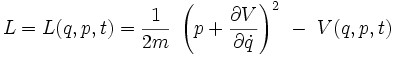
- En développant le carré, on obtient:
Dans le lagrangien
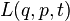
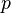
Avec l'impulsion comme variable, les équations d'Euler-Lagrange ne changent pas de forme :
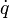
- Introduction - Historique - Définition du lagrangien et de l'action classiques - Une alternative de présentation - L'équation fondamentale de la dynamique newtonienne - Équation d'Euler-Lagrange - Particule chargée dans un champ électromagnétique - Cas où il y a des forces de frottements - Invariances et constantes du mouvement - L'impulsion