Principe de moindre action et mécanique classique - Définition

Introduction

En mécanique classique, le principe de moindre action est très utilisé pour déterminer les trajectoires et états des systèmes physiques.

L'action se présente comme la sommation, le long du parcours du système, de la différence entre l'énergie cinétique et l'énergie potentielle. La détermination du trajet se fait par une méthode variationnelle : à points extremum fixés, temps de trajet fixé, et trajet variable, on cherche le ou les trajets pour lesquels l'action est stationnaire par rapport aux variations possibles et infimes du trajet.

Cette méthode aboutit aux équations d'Euler-Lagrange qui donnent des trajets sur lesquels l'action n'est pas toujours minimale, mais parfois maximale, voire ni l'un ni l'autre mais seulement stationnaire. Dans tous les cas ces trajets respectent les conditions physiques et sont donc réalistes. Mais le long de chacun de ces trajets, si deux points sont assez proches (mesure faite par la longueur du trajet les séparant) alors on peut démontrer qu'entre eux ce trajet minimise l'action dans la méthode variationnelle, ce qui justifie le nom du principe.

On peut interpréter cela comme équivalent aux deux conditions suivantes :

• la trajectoire que suit un corps est celle qui permet la transformation instantanée de l'énergie cinétique en énergie potentielle la plus petite possible (donc aussi la plus lente sur la trajectoire), ou la transformation immédiate dans le sens inverse la plus grande possible (donc la plus rapide possible sur la trajectoire) ;
• la transformation (et donc la trajectoire) est déterminée par les conditions initiales (position et vitesse) et les conditions de l'environnement physique : il doit y avoir continuité de la trajectoire s'il y a continuité du milieu physique.

Il y a parfois un échange cyclique entre ces deux énergies (balancier sans frottement, satellite à orbite elliptique...) ou une stabilisation provisoire (bille immobile ou posée au fond d'un trou, satellite à orbite circulaire...).

La chute libre d'un corps est l'exemple type de la transformation de l'énergie potentielle (gravitationnelle) en énergie cinétique. Le ralentissement et l'arrêt (avant sa chute) d'un corps lancé verticalement est un exemple de la transformation inverse.

Les frottements imposent une transformation plus compliquée car ils engendrent de la chaleur, qui est l'énergie cinétique des molécules des matériaux, mais en négligeant cette forme d'énergie, on peut utiliser le Principe de moindre action en considérant que de l'énergie cinétique se perd (sort du système étudié).

Historique

Pierre de Fermat s'intéressait au problème du chemin pris par la lumière, dans une simplification similaire à l'optique géométrique, et notamment au trajet le plus court en temps que celle-ci prend lors d'une transition de milieu, précisant que la lumière prend le chemin le plus court et non pas la distance la plus courte (cf temps de parcours du chemin). Maupertuis répond que les corps massifs prennent le chemin où leur quantité d'action est localement minimisée, d'où le nom de principe de moindre action (1744). En 1788 Lagrange (mathématicien français) propose une formulation mathématique du principe de moindre action et qui est encore en vigueur de nos jours.

Définition du lagrangien et de l'action classiques

Considérons pour simplifier un point matériel décrit, dans un repère galiléen, par un seul degré de liberté, noté q(t) à l'instant t. Le lagrangien est la différence entre l'énergie cinétique (du point matériel) et l'énergie potentielle (due à l'environnement physique) :

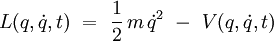
où est l'énergie cinétique du système et est l'énergie potentielle, qui en général ne dépend pas de .

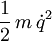
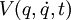
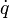
L'action de la trajectoire, étant la somme totale de la différence entre l'énergie cinétique et l'énergie potentielle durant la trajectoire, est définie par:

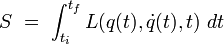
où t_i et t_f désignent respectivement l'instant initial et l'instant final.