Principe de moindre action et mécanique classique - Définition
La liste des auteurs de cet article est disponible ici.
Une alternative de présentation
- Soit on expose l'action et le lagrangien habituels de la physique classique (non relativiste), puis on détermine les équations d'Euler-Lagrange.
- Soit on définit abstraitement l'action et le lagrangien (à la manière de Landau et Lifchitz), et on détermine leurs formes et leurs propriétés qu'imposent les principes de la physique, ainsi que les équations d'Euler-Lagrange.
Dans cet article, seule la première présentation sera donnée.
L'équation fondamentale de la dynamique newtonienne
Supposons que
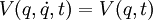
Avec l'expression du lagrangien classique, on obtient:
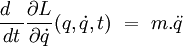
Les équations d'Euler-lagrange donnent:
|
|
Ce qui exprime les lois du mouvement de Newton avec:
| (Somme des forces extérieures) =
|
Si toutes les forces en jeu dérivent d'un potentiel, le principe de moindre action peut être considéré comme une réécriture des lois du mouvement de Newton.
Équation d'Euler-Lagrange
- Dire que le chemin « minimise localement l'action » signifie que pour tout autre chemin ayant les mêmes conditions initiales et finales, et suffisamment proche du chemin minimisant, la valeur de l'action est plus grande.
- Avec certaines conditions initiales et/ou finales, le chemin minimisant localement l'action peut ne pas exister, mais s'il existe, il est unique (à cause des conditions initiales et de la continuité du mouvement).
Le lagrangien n'est pas défini de manière unique : l'ajout au lagrangien d'une fonction
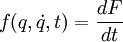
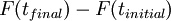
Le chemin q(t) effectivement suivi par le point matériel entre les instants ti et tf fixés est un extremum de l'action (car il lui fait atteindre sa valeur minimale), donc en faisant une variation du chemin, on a :
|
|
L'équation (d'Euler-Lagrange) que l'on en déduit sont:
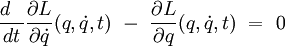
La démonstration se trouve dans l'article détaillé.
Particule chargée dans un champ électromagnétique
Ici

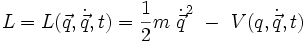
avec :
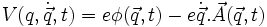
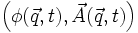
Donc :
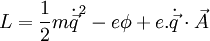
En posant
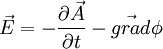
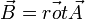
Les équations d'Euler-Lagrange donnent :
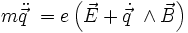
Où est appelé force de Lorentz.
Historiquement, la force de Lorentz a été trouvée avant l'idée du potentiel électromagnétique.
Cas où il y a des forces de frottements
On suppose que le système évolue dans un milieu homogène (mêmes propriétés à tous les endroits) et isotrope (mêmes propriétés dans toutes les directions), et dont la viscosité engendre des frottements :
- S'il n'y a qu'un seul degré de liberté
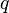
- En première approximation, les forces de frottements peuvent se modéliser par
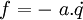
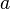

- On peut donc utiliser le potentiel
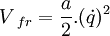
- S'il y a plusieurs degrés de liberté, le lagrangien s'écrit
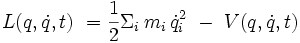
- Et la force de frottement dans la direction de la j-ième coordonnée est
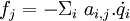
- Ce qui est une égalité scalaire, où les
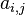
- Il n'y a de potentiel que si
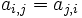
- Dans le cas où il y a un potentiel (appelé fonction de dissipation), il a la forme d'une fonction quadratique :
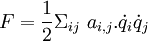
- On vérifie facilement que :
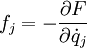
- Dans tous les cas, pour préserver l'utilisation du lagrangien, et pour respecter l'équation fondamentale de la dynamique, on écrit :
-
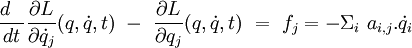
Si la fonction de dissipation
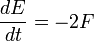
Pour une vue plus exhaustive sur les frottements, consulter le wikilivre Tribologie
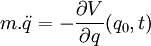
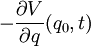
![\delta S[q] \ = \ 0](https://static.techno-science.net/illustration/Definitions/autres/5/5cf148f87ee7c4f2c18c465a32fbe577_e66845dc57b5627b77e29f3e996298b1.png)

















































