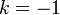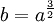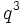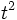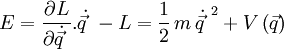Principe de moindre action et mécanique classique - Définition

Invariances et constantes du mouvement

Le théorème de Noether montre qu'une invariance du lagrangien par une transformation impose une grandeur invariante du système. On peut utiliser l'énergie du système pour arriver aux mêmes invariants (mis à part le premier cas).

Indépendance par rapport au temps

Si les forces en présence sont indépendantes du temps ou si le système est fermé, alors le lagrangien ne dépend pas explicitement du temps : ou encore

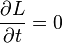
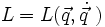
En dérivant le lagrangien par rapport au temps, on démontre que l'énergie totale

C’est-à-dire :

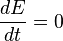
Ceci peut se démontrer directement à partir de l'équation fondamentale de la dynamique.

L'énergie du système peut aussi être définie comme la transformée de Legendre du lagrangien.

Dans le cas particulier où il s'agit d'un potentiel électromagnétique, et en utilisant les notations vues ci-dessus pour ce cas, on montre que :

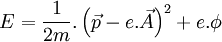
Translation dans l'espace

Pour un système fermé, et du fait de l'homogénéité (mêmes propriétés à des endroits différents) de l'espace, une translation du système de vecteur constant n'en change pas les propriétés, et donc ne change pas le lagrangien.

On en tire la conclusion de l'invariance de l'impulsion du système. Cette impulsion est la somme des impulsions des éléments du système.

Rotation dans l'espace

Pour un système fermé, et du fait de l'isotropie de l'espace (mêmes propriétés dans des directions différentes) de l'espace, une rotation fixée du système n'en change pas les propriétés, et donc ne change pas le lagrangien.

On en tire la conclusion de l'invariance du moment cinétique du système. Ce moment cinétique est la somme des moments cinétiques des éléments du système.

Changement de repère galiléen

Un changement de repère galiléen ne change pas les propriétés du système, par contre il permet de montrer qu'il existe un centre de masse (ou centre d'inertie) du système : particule virtuelle dont la masse est la masse totale du système, et animée d'un mouvement rectiligne uniforme en cas d'absence d'interaction avec l'extérieur.

Dans ce dernier cas, en posant

• = masse totale
• = vitesse du centre de masse
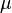
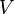
• énergie interne :
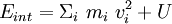
• lagrangien interne :

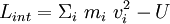
avec = vitesse relative du ième corps par rapport au centre de masse

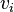
et = énergie potentielle d'interactions entre les corps du système.

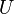
Le lagrangien du système peut s'écrire :

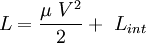
et l'énergie

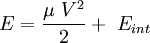
Le référentiel à privilégier pour faciliter les calculs est le référentiel du centre de masse dont l'impulsion et le moment cinétique sont ceux vus ci-dessus.

Changement de jauge

La jauge est l'ensemble des unités de mesures utilisées pour mesurer les différentes caractéristiques du système. Un changement de jauge qui ne change le lagrangien que d'un facteur multiplicatif constant permet de montrer facilement certaines propriétés quand l'énergie potentielle est une fonction homogène des coordonnées (ce qui est souvent le cas).

Plus précisément : supposons que

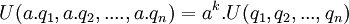
Un changement global de jauge est un changement de mesures : et

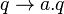
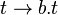
Ce qui signifie que : et où , d'une part, et et de l'autre, sont des mesures différentes des mêmes distances physiques ou temporelles.

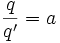
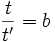
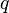
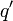
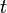
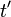
Alors subit le changement de mesure , donc l'énergie cinétique subit un changement de mesures de facteur

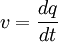
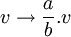
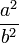
Pour que le lagrangien ne soit que multiplié par un nombre constant, il faut que : , c'est-à-dire :

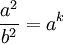
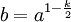
• Par exemple avec le potentiel gravitationnel newtonien, on a : , donc , c'est-à-dire : proportionnel à , ce qui correspond à la 3^e loi de Kepler.