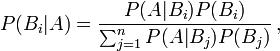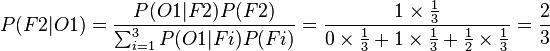Problème de Monty Hall - Définition
La liste des auteurs de cet article est disponible ici.
Résolution par le théorème de Bayes
L'énoncé renvoie en définitive à un problème de probabilité conditionnelle et selon la formulation générale du théorème de Bayes :
- Soit A un évènement quelconque,
- Soit B1,B2,...,Bn est un ensemble d'évènements à la fois exhaustifs et mutuellement exclusifs,
Alors pour tout i, on a :
Une application du théorème de Bayes au problème de Monty Hall pourrait être formulée ainsi :
Considérons le cas où la porte 3 a été choisie et aucune porte n'est encore ouverte. La probabilité que la voiture soit derrière la porte 2 p(F2) est de 1/3, probabilité qui serait en outre exactement la même pour chaque porte.
La probabilité que le présentateur ouvre la porte 1 p(O1) est alors de 1/2. En effet, le candidat ayant choisi la porte 3 et le présentateur sachant ce que cache chaque porte :
- Soit la voiture est derrière la porte 1 : le présentateur ouvrira la porte 2.
- Soit la voiture est derrière la porte 2 : le présentateur ouvrira la porte 1.
- Soit la voiture est derrière la porte 3 : le présentateur ouvrira la porte 1 ou le présentateur ouvrira la porte 2 (équiprobabilité 1/2)
La probabilité que le présentateur ouvre la porte 1 sachant que la voiture est derrière la porte 2 est donc p(O1|F2) = 1. La possibilité que la voiture soit derrière la porte 2 sachant que le présentateur ouvre la porte 1 est donc :
Au cinéma
Dans le film Las Vegas 21, un film de blackjack, un professeur du MIT de Boston demande à son étudiant de résoudre le problème de Monty Hall pour voir s'il est assez bon pour rejoindre son club de blackjack. L'élève répond qu'il y a deux fois plus de chances avec un changement, ce qui est une bonne réponse.
On retrouve également ce problème dans l'épisode 13 de la première saison de la série NUMB3RS, quand le professeur de mathématiques Charlie Eppes (interprété par David Krumholtz) tente de l'enseigner à ses élèves.
Dans la littérature
L'écrivain et scénariste britannique Mark Haddon expose et démontre le Problème de Monty Hall dans son roman le Bizarre Incident du chien pendant la nuit ainsi que Bernard Werber à plusieurs reprise dans ses opus. Néanmoins ni l'un ni l'autre ne sont mathématiciens, et Bernard Werber a commis plus d'une erreur dans ses ouvrages, qui ne se veulent que récréatifs.