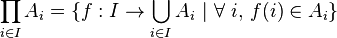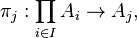Produit cartésien - Définition

Produits infinis

On peut généraliser la notion de produit cartésien à celle de produit d'une famille d'ensembles indexée par un ensemble quelconque, fini ou infini.

Bien que plus générale, cette notion peut difficilement être introduite en théorie des ensembles avant celle de produit cartésien binaire, du moins naturellement, car elle fait appel à la notion de fonction, qui utilise à son tour justement celle de couple, et donc de produit cartésien binaire.

Famille d'ensembles

Une famille A d'ensembles indexée par un ensemble I est une fonction définie sur I. L'image de i par A est notée A_i. Il s'agit juste d'une notation (adaptée à un certain usage) pour une construction connue.

• La famille A indexée par I sera plutôt notée . Au sens de la théorie des ensembles, la famille peut être assimilée à son graphe, l'ensemble des couples ( i, A_i ), pour .

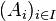
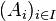
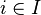
• Toutefois, la réunion d'une famille , notée , désigne bien la réunion des images A_i de la famille en tant que fonction, et non celle des éléments de la famille en tant que graphe, qui sont au sens strict les couples ( i, A_i ).

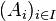
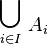
Produit cartésien d'une famille d'ensembles

On peut maintenant définir le produit cartésien d'une famille d'ensembles , que l'on note habituellement , ou parfois .

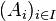
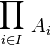
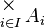
Il s'agit de l'ensemble des fonctions f de I dans la réunion de la famille, telles que pour tout i dans I, f(i) appartienne à A_i :

• Pour utiliser cette définition, il faut pouvoir extraire d'un élément du produit sa composante d'index j, élément de I.

Pour cela, on définit pour tout j dans I, la fonction appelée j-ème projection,

par :

.

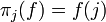
• On peut énoncer l'axiome du choix ainsi : le produit d'une famille d'ensembles non vides est non vide.