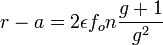Profondeur de champ - Définition

Cas particulier de la macrophotographie

Lorsque l'on photographie un paysage, une scène de rue, dans une moindre mesure un nu ou un repas de famille, la taille de l'image est très petite par rapport à la taille du sujet et le grandissement prend une valeur proche de 1. L'image se forme à une distance du centre optique ou du point nodal image très légèrement supérieure à la distance focale. Il n'en est pas de même en proxiphotographie et surtout en macrophotographie qui est un domaine où, par définition, l'image a des dimensions égales ou supérieures à celles du sujet.

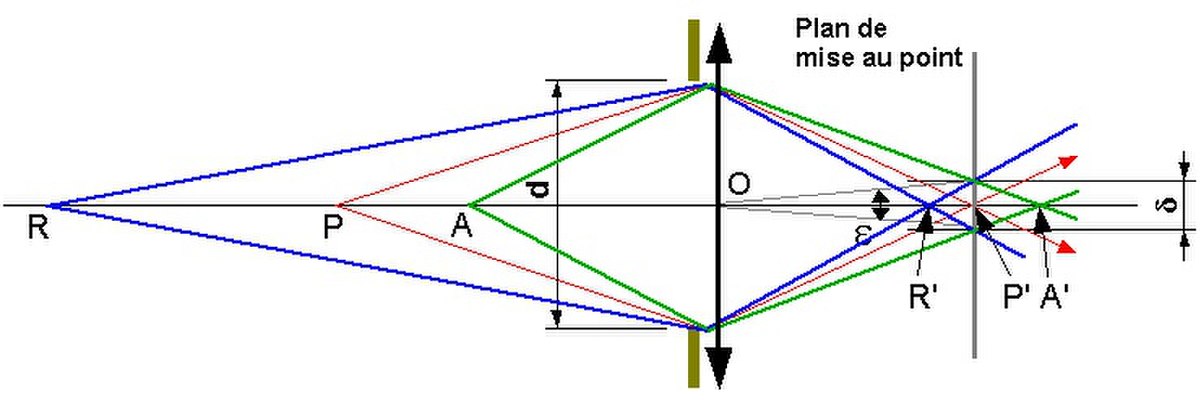
Le schéma qui nous a servi à établir les formules théoriques de la profondeur de champ correspondait en fait à une situation relevant de la proxiphotographie.

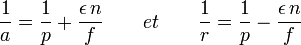
Les deux formules générales que nous avons précédemment établies restent évidemment valables pour un examen de l'image finale depuis la distance orthoscopique.

Entre la photographie des sujets de taille importante et celle des sujets minuscules, il existe une différence fondamentale qui n'est pourtant presque jamais signalée dans la littérature photographique :

• Les grands objets sont généralement plus ou moins familiers car on les côtoie, on vit éventuellement au milieu d'eux, on connaît leurs formes et leurs propriétés. C'est ainsi qu'en examinant des photographies où apparaissent des êtres humains, des arbres, des bâtiments, des animaux domestiques, etc., il est assez facile de restituer mentalement la disposition des éléments dans l'espace, d'évaluer leurs dimensions respectives ou de détecter d'éventuelles disproportions.
• Les très petits objets, en revanche, demandent qu'on les découvre avant d'aller plus loin. Pour ce faire, une photographie n'est pas forcément la meilleure solution, d'autant qu'elle peut souvent être très ambiguë et donner une idée très fausse de la réalité. La troisième dimension, qui réapparaît grâce à la vision binoculaire ou à la stéréophotographie, permet de lever les doutes et parfois, de s'apercevoir que la façon dont on s'imaginait un objet à partir d'une photo était complètement erronée ! Autrement dit, l'œil n'a plus de repère et généralement, quand on lui présente une macrophotographie à diverses distances, il est absolument incapable d'en ressentir les éventuelles déformations liées au non respect de la distance orthoscopique.

On se trouve donc devant une alternative : ou bien la macrophotographie est destinée à un usage scientifique, il faut alors retrouver la distance orthoscopique exacte, surtout si l'on doit procéder à des mesures de dimensions ; ou bien elle n'a qu'un but d'illustration, artistique ou non, et dans ce cas la distance d'observation importe peu.

C'est pourquoi nous supposerons que l'image est examinée depuis une distance égale à sa diagonale, selon une procédure désormais habituelle, et nous corrigerons en conséquence la netteté conventionnelle.

• première correction : si la prise de vue se fait avec un objectif de focale normale f, l'allongement du tirage n'est plus négligeable, l'image se formant à une distance p' du centre optique telle que p'=f(g+1). La distance orthoscopique n'est plus D mais D(g+1).
• seconde correction : si la photo est prise avec une focale f différente de f la distance orthoscopique doit être multipliée par f/f.

Nous allons en tenir compte directement en modifiant en conséquence l'angle limite de netteté :

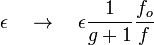
Il en résulte que :

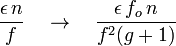
La transformation des formules générales donne alors :

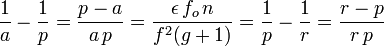
Dans les conditions qui sont ici les nôtres, les trois valeurs a, r et p sont très voisines, de sorte que l'on peut écrire avec une très bonne approximation :

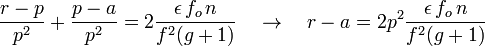
En remplaçant p par sa valeur en fonction du grandissement , il vient :

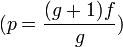
Pour un format de négatif donné, lorsque l'image finale est examinée depuis une distance égale à sa diagonale, la profondeur de champ dépend du agrandissement souhaité lors de la prise de vue et de l'ouverture du diaphragme mais pas de la focale de l'objectif utilisé pour la prise de vue. Rappelons que la focale normale f est égale à la diagonale du format.

Amateurs de calculs, attention ! La plupart des objectifs « macro » modernes, en particulier ceux qui permettent d'atteindre directement le rapport 1, sont en réalité des zooms. L'augmentation du grandissement se fait à la fois par augmentation du tirage (l'objectif avance par rapport à l'appareil) et par diminution de la distance focale. Ainsi, un objectif «macro» de 90 mm de focale sera bien un 90 mm pour les mises au point lointaines (excellent pour le portrait) mais deviendra un objectif de 60 ou 55 mm au rapport 1. En cas de besoin, les fabricants sont en mesure de préciser la loi de variation et le déplacement des points nodaux.

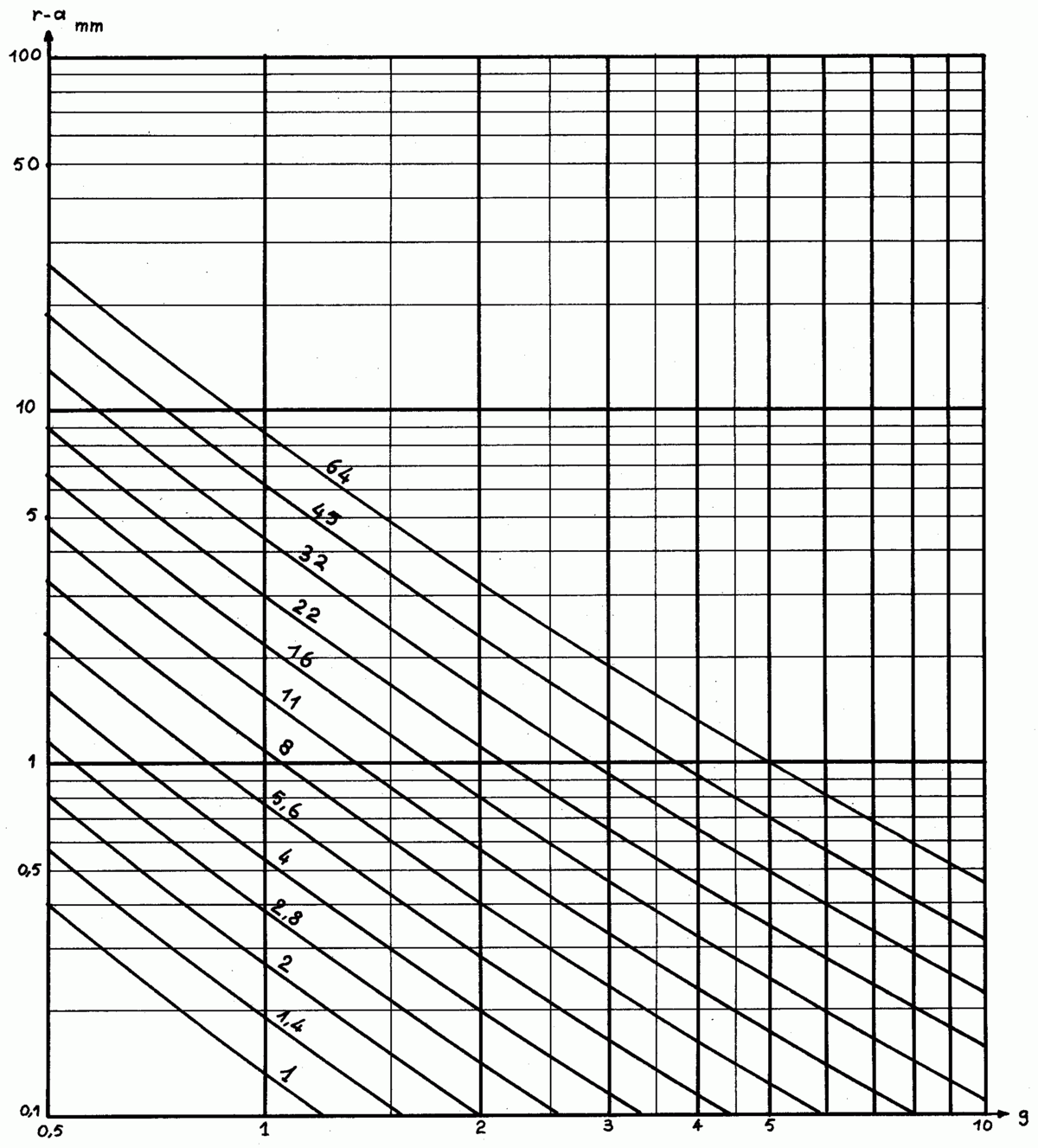
L'abaque ci-dessous donne directement la profondeur de champ r-a pour le format 24x36 en fonction du rapport de agrandissement souhaité et de l'ouverture du diaphragme. En cliquant on accède à la version haute définition directement imprimable.

Abaque pour prise de photos en macro.

La profondeur de champ augmente quand le format de prise de vue diminue. Supposons réalisées les conditions suivantes :

• l'objectif de prise de vue est parfait ;
• l'agrandissement de l'image enregistrée pour donner l'image finale qui sera examinée ne cause aucune perte.

Au lieu d'un format 24x36, utilisons par exemple un format 12x18. La focale normale passera, pour faire simple, de 50 à 25 mm. Le grandissement à la prise de vue sera deux fois plus petit, mais l'image obtenue devra ensuite être agrandie deux fois plus.

Avec un diaphragme de 16 et un grandissement de 1, le format 24x36 donnera une profondeur de champ de :

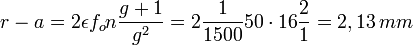
Cette valeur peut être lue directement sur l'abaque.

Avec le même diaphragme et un grandissement de 0,5, le format 12x18 donnera une valeur nettement supérieure :

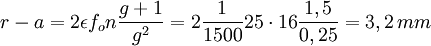
Avec du film, la diminution exagérée du format de prise de vue posait de nombreux problèmes : grain et défauts divers de l'émulsion, risque de rayures, etc., et l'agrandissement plus important altérait davantage l'image. Les conditions ont changé avec l'apparition des capteurs numériques de petit format, liée à une augmentation considérable mais discrète de la qualité des objectifs, qui sont de plus petite taille et plus faciles à fabriquer. La plupart des amateurs de macrophotographie sont désormais passés à la prise de vue numérique, mais ceci est une autre histoire.