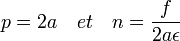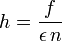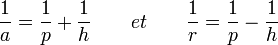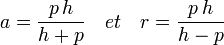Profondeur de champ - Définition

Introduction

Une courte profondeur de champ

Pour un réglage et une utilisation donnés d'un appareil photographique, la profondeur de champ correspond à la zone de l'espace dans laquelle doit se trouver le sujet à photographier pour que l'on puisse en obtenir une image que l'œil (ou un autre système optique) acceptera comme nette.

L'étendue de cette zone dépend des paramètres de la prise de vue ; notamment de la distance de mise au point, de l'ouverture du diaphragme et des dimensions de la surface sensible. La connaissance de la profondeur de champ est nécessaire à la maitrise des prises de vues, en photographie comme en cinéma et en vidéo. Dans la pratique, le contrôle de la profondeur de champ est important pour mettre en valeur un sujet dans les techniques de portrait, de paysage et de nature morte. Plus la profondeur de champ est étendue, plus elle intègre le sujet dans son environnement. A contrario, plus elle est courte, plus elle l'isole. Les plans en avant et en arrière du sujet seront alors plus ou moins flous.

Résumé

• Plus on ferme le diaphragme, plus la profondeur de champ est grande, mais plus la diffraction dégrade l'image.
• Au mieux, le pouvoir séparateur angulaire de l'œil permet de distinguer des détails de 0,33 mm à 1 m, ou de 3,3 mm à 10 m, etc., ce qui correspond à un angle d'environ 1/3000 radian. Pour les applications courantes, on adopte plutôt 1/1 500 radian. Un manque de contraste donne l'impression trompeuse d'un manque de netteté.
• L'iris de l'œil et le diaphragme de l'appareil photo n'ont pas du tout les mêmes fonctions et il faut se méfier de toute comparaison abusive.
• Si la mise au point est faite sur l'infini, tout paraît net au-delà d'une certaine distance, en deçà de l'infini, dite distance « hyperfocale », qui varie avec l'ouverture du diaphragme et la focale de l'objectif. Si la netteté doit s'étendre d'une distance a jusqu'à l'infini, il faut régler la mise au point sur 2a (distance hyperfocale) et déterminer l'ouverture du diaphragme en fonction du degré de netteté souhaité. Les appareils à mise au point fixe sont calés sur l'hyperfocale.
• Les échelles de profondeur de champ gravées sur les objectifs sont fort utiles, quand elles existent. Le testeur de profondeur de champ permet de fermer manuellement le diaphragme à une valeur donnée et de contrôler l'étendue de la profondeur de champ afin de choisir l'ouverture de diaphragme optimum pour une profondeur de champ désirée.
• Un objectif de longue focale ne permet pas de s'approcher du sujet mais il permet de n'en voir qu'un détail en limitant l'angle de champ de la prise de vue.
• En macrophotographie, l'œil perd ses repères d'appréciation de la perspective. Pour un format de négatif ou de capteur donné, lorsque l'image finale est examinée depuis une distance égale à sa diagonale, la profondeur de champ dépend du grandissement à la prise de vue et de l'ouverture du diaphragme mais pas de la focale de l'objectif utilisé. Elle augmente quand le format de prise de vue diminue.

Distance hyperfocale

La profondeur de champ s'étend normalement entre une limite proche et une limite lointaine. Que se passe-t-il lorsque la seconde se trouve rejetée à l'infini ?

En reprenant les formules,

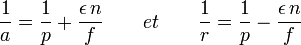
Si r tend vers l'infini, la seconde donne :

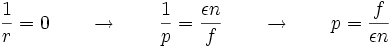
Le report de p dans la première fournit la relation avec a :

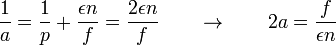
Finalement :

Il en résulte que si la netteté doit s'étendre d'une distance a jusqu'à l'infini :

• la première chose à faire est de régler la mise au point sur 2a ;
• la seconde est de déterminer l'ouverture du diaphragme en fonction du degré de netteté souhaité.

Avec un objectif de 50 mm de focale (0,05 m), une profondeur de champ s'étendant de 5 m à l'infini et une limite de netteté de 1/1500, la mise au point sera faite sur 10 m et le diaphragme à prendre sera :

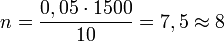
C'est bien ce qui est indiqué sur l'échelle de profondeur de champ :

Échelle de profondeur de champ : 8

En passant au diaphragme 16, les distances peuvent être divisées par 2 et, avec une mise au point sur 5 m, la netteté obtenue s'étendra de 2,5 m jusqu'à l'infini.

La netteté obtenue s'étendra de 2,5 m jusqu'à l'infini.

Par convention, on appelle distance hyperfocale la quantité :

Contrairement à la focale, l'hyperfocale ne caractérise pas un objectif donné, mais un ensemble de trois paramètres que sont la focale, l'ouverture du diaphragme et le degré de netteté choisi arbitrairement (ce qui ne veut pas dire au hasard !).

Lorsque l'on met au point sur l'infini, la netteté commence à l'hyperfocale. Sur l'échelle de profondeur de champ de notre objectif, h se lit directement en face des graduations du diaphragme.

Au diaphragme 16, mise au point faite sur l'infini, la netteté commence à 5 mètres.

On lit 5 m à 16, 10 m à 8 et, en prolongeant la série, on déduit 20 m à 4 ou 40 m à 2, ouverture maximale de cet objectif.

Au diaphragme 16, mise au point faite sur l'infini, la netteté commence à 5 m. En mettant au point sur 5 m, elle s'étend de 2,5 m à l'infini. Le fait de mettre au point sur l'infini est presque toujours une erreur et constitue, d'une certaine manière, un « gaspillage » des possibilités de l'objectif. Pour un paysage, par exemple, l'œil est très exigeant pour la netteté des objets situés à quelques mètres ou dizaines de mètres mais beaucoup plus tolérant pour celle des lointains, ce qui rend encore plus logique une mise au point au voisinage de l'hyperfocale.

Une mise au point a priori sur l'hyperfocale a permis à beaucoup de grands photographes, par le passé, de gagner un temps précieux lorsqu'ils faisaient des photos sur le vif : ils n'avaient ainsi plus besoin de se préoccuper de la mise au point. Aujourd'hui, cette notion est toujours utile aux photographes qui ont l'habitude d'opérer avec un appareil non automatique ou avec un automatisme à priorité diaphragme : même si l'appareil se charge de la mise au point, le fait de fixer le diaphragme pour disposer dans tous les cas d'une profondeur de champ suffisante améliore les chances de réussite.

Les appareils à mise au point fixe sont réglés une fois pour toute sur l'hyperfocale qui correspond à la plus grande ouverture de leur diaphragme. Il faut donc s'attendre à ce qu'ils donnent leurs moins mauvais résultats à des distances de l'ordre de 3 à 5 m.

Enfin, en fonction de h, les formules de la profondeur de champ s'écrivent sous une forme qui n'est pas sans rappeler la formule de Snell-Descartes :

ou si l'on préfère :