Profondeur de champ - Définition

Problèmes liés au non respect de la distance orthoscopique

Lorsque l'on enseigne la perspective à des étudiants en architecture, il faut non seulement leur apprendre à tracer convenablement les diverses vues qu'ils montreront à leurs clients, mais aussi leur montrer comment, à partir de documents à deux dimensions, il est possible de restituer la disposition des objets dans l'espace. Il faut connaître pour cela un nombre minimum de données géométriques, sans quoi rien n'est possible.

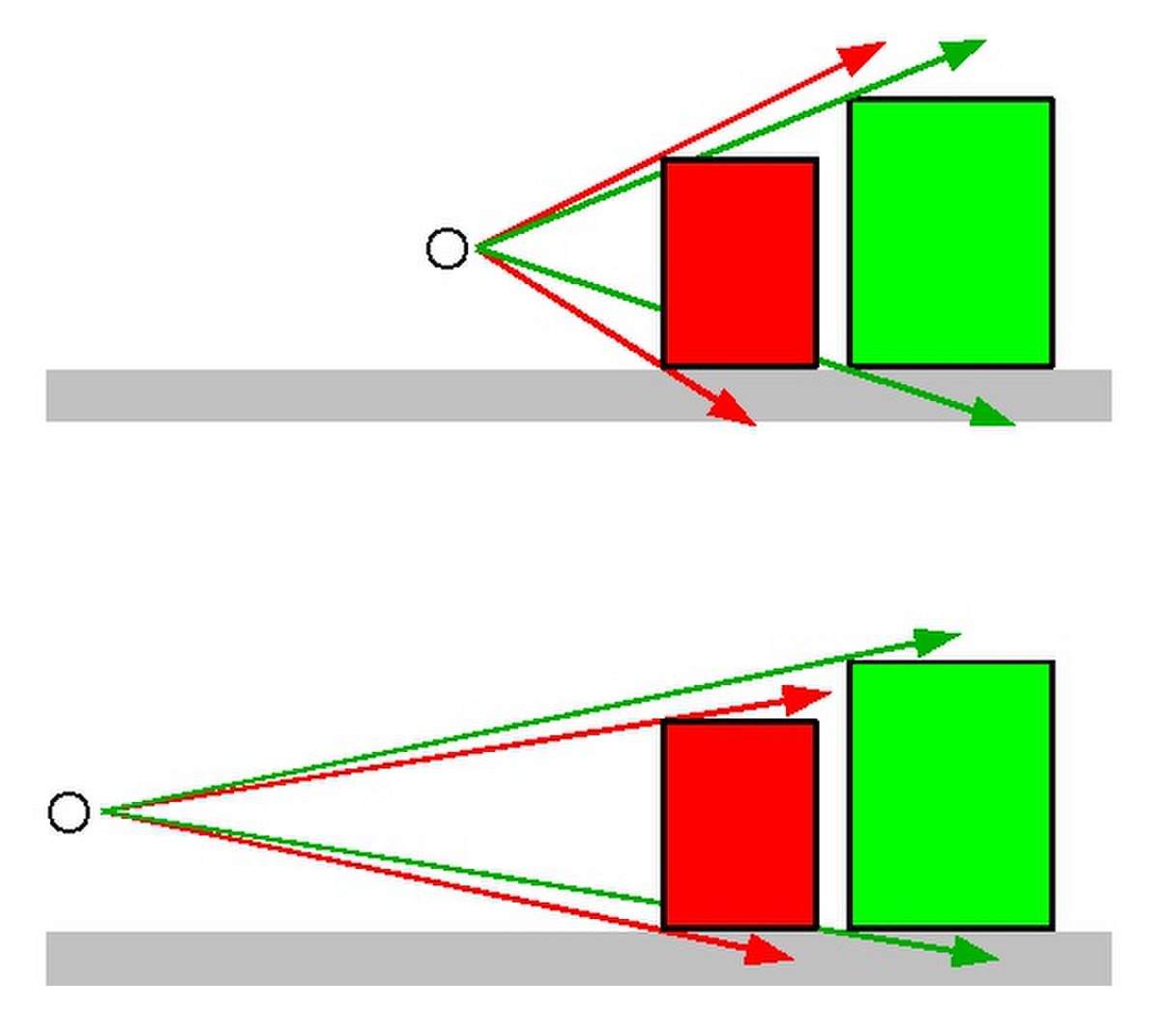
Ici, le jeu pourrait consister à retrouver la hauteur du tonnelet rouge, sachant que celle du tonnelet vert est de 9 cm et que les deux jouets sont posés sur un même plan horizontal. Il n'est pas gagné d'avance.

A : grand-angulaire

B : téléobjectif

Sur les deux photos A et B, l'avant du tonnelet vert a la même hauteur ; sur la photo B, les deux tonnelets ont la même hauteur. Un point de vue plus ou moins éloigné modifie les dimensions relatives, mais ce n'est pas tout, il modifie aussi les formes : les cercles sont vus sous la forme d'ellipses beaucoup plus aplaties sur la photo B que sur la photo A.

Effet de l'éloignement sur la taille apparente des objets photographiés.

Si l'on veut qu'une photographie restitue aussi complètement que possible la réalité, il faut l'examiner sous un angle identique à celui sous lequel le sujet était vu lors du déclenchement. Le tonnelet rouge a l'air un peu bizarre sur la photo A, qui retrouverait un aspect naturel si on l'examinait depuis une distance un peu inférieure à sa largeur, soit environ 9 cm sur un écran de 19 pouces. Il y a une justice pour les myopes. Pour avoir l'air naturelle, la photo B devrait être regardée d'une distance égale à environ deux fois sa diagonale, environ 25 cm sur le même écran. De très près, elle prend évidemment un allure bizarre et de très loin, elle donne l'impression que les deux tonnelets sont identiques mais posés à des hauteurs différentes.

Notre cerveau, en travaillant, finira par nous convaincre que le tonneau rouge est moins haut que le vert. En fait, il mesure 7 cm.

Le respect rigoureux de l'angle de prise de vue est souvent difficile, voire impossible. Imaginons un immeuble de 10 m de hauteur photographié depuis une distance de 150 m. Si, sur une photographie de format 20x30 cm, son image mesure 10 cm, alors la distance d'observation doit être également divisée par 100, ce qui donne 1,5 m. Le spectateur, n'ayant vraisemblablement pas les bras assez longs, devra poser la photo sur un support et prendre du recul. Si les photos ont été prises avec un téléobjectif puissant, il devra les regarder d'encore plus loin et, si elles ont été prises de très près avec un grand-angulaire extrême, il faudra qu'il y colle le nez.

Mieux : dans une salle où l'on projette des diapositives, tous les spectateurs devraient occuper le même siège et en changer à chaque fois que le photographe a changé de focale...

Mais que se passe-t-il dans la vie réelle ?

• Les photographies de format « carte postale » ou plus petites sont presque toujours regardées de beaucoup trop loin, de sorte que beaucoup de leurs défauts passent inaperçus. Notre étude ne s'y applique guère et d'ailleurs, comme les statistiques le prouvent, ces « souvenirs » finissent en général au fond d'un tiroir, après qu'on les a regardés deux ou trois fois : trop peu de photographes prennent le temps d'annoter soigneusement leurs photos et de choisir celles qu'ils vont archiver.
• Vous verrez parfois, dans des expositions plus ou moins prestigieuses, des photos minuscules montées sur des fonds blancs démesurés. C'est à la mode mais cette façon de faire, que l'on ne devrait jamais conseiller à des débutants car elle les empêche de progresser, est a priori suspecte quand elle devient systématique. L'œil est irrésistiblement attiré pas les zones claires d'une scène et le cadre prend alors le pas sur la photo, qui paraît alors plus sombre. Cet effet renforce celui du format trop petit, vu de trop loin, pour masquer les défauts d'une image.
• Les œuvres de ceux qui font « de la photo », et non « des photos », ont été sélectionnées avec soin et agrandies dans un format plus confortable, par exemple 20x30 cm. On les observe instinctivement depuis une distance à peu près égale à leur diagonale, ce qui correspond au champ visuel réputé « normal » du genre humain. Selon ce principe, une image de 24x36 cm est regardée depuis une distance d'environ 43 cm. Pour un photographe d'âge mûr, c'est plutôt 50 cm car au fil du temps le champ visuel se rétrécit et la vision de près se dégrade. Cette distance, toujours à peu près la même, ne tient pas compte de la focale utilisée pour la prise de vue. Elle permet de conserver assez bien l'angle de vision si le photographe a utilisé, en format 24x36 mm, une focale dite normale de 45 à 50 mm, sinon, les problèmes apparaissent !

Appelons f la focale « normale » correspondant au format de l'image enregistrée (43 mm pour le 24x36, 85 mm pour le 6x6, etc.) et D la diagonale d'un agrandissement homothétique de cette image, sur papier ou sur écran. Le second grandissement sera bien sûr :

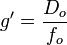
La focale réellement utilisée à la prise de vue peut être exprimée en fonction de la focale normale, la distance orthoscopique variera dans le même rapport en fonction de D :

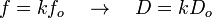
Naturellement, si la distance orthoscopique n'est pas respectée, l'appréciation de la netteté se trouvera profondément modifiée et avec elle, la profondeur de champ apparente.

Photographie au téléobjectif

Un objectif de grande distance focale ne permet en aucun cas de s'approcher du sujet, en revanche il fournit une image plus grande que si l'on utilisait une focale « normale ».

Dans ce cas la photographie finale est généralement regardée de beaucoup trop près. Un agrandissement de 20x30 cm obtenu à partir d'un négatif de 24x36 mm (g' = 200/24) et d'un objectif de 300 mm devrait être regardé depuis une distance :

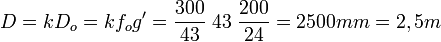
Cette distance est évidemment beaucoup plus grande que celle qui sera généralement observée dans la réalité. Le spectateur va se rapprocher de l'image et donc percevoir comme flous des détails qui, vus à la distance orthoscopique, apparaîtraient nets. Concrètement, si l'on se place à 50 cm au lieu de 2,5 m, il faudra être 5 fois plus exigeant sur la netteté et donc adopter comme limite angulaire non plus 1/1500 mais 1/7500, ce qui change beaucoup de choses.

• Pour un objectif de focale normale, une bonne qualité optique peut suffire. Pour un téléobjectif, il faut atteindre l'excellence pour que les résultats soient à la hauteur.
• L'image étant regardée de beaucoup trop près, les divers plans donnent l'impression assez désagréable d'être "tassés". Pour éviter cette impression, on peut suggérer de faire une mise au point impeccable sur le sujet principal en laissant tout le reste flou. Un seul plan bien mis en valeur vaut mieux que plusieurs défectueux ; les grandes photos sont souvent les plus simples.
• Un téléobjectif à la fois ouvert et très bon dès la pleine ouverture permettra d'augmenter le flou là où il faut, en diminuant la profondeur de champ, et d'éviter au contraire le flou dû à la mauvaise qualité optique et aux « bougés » (le bougé de l'appareil et celui du sujet, si celui-ci est mobile).

On comprend mieux dès lors pourquoi un téléobjectif à la fois puissant, lumineux et surtout de bonne qualité dès la pleine ouverture atteint facilement le coût d'une petite voiture.

Photographie au grand-angulaire

Un objectif grand-angulaire oblige à se tenir très près du sujet, sinon celui-ci n'occupe sur l'image qu'une place insignifiante. Nous parlons ici des véritables objectifs grand-angulaires, qui sont exempts de distorsion, et non des objectifs de type « fish-eye ». Sans grand risque d'erreur, nous pouvons déjà inverser toutes les propositions précédentes.

Un agrandissement de 24x36 cm réalisé d'après un négatif de 24x36 mm posé derrière un objectif de 17 mm doit normalement être observé à 17 cm au lieu des 45 ou 50 habituels. Il est évident que la photographie résultante sera presque toujours observée de trop loin.

• Un objectif médiocre donnera donc facilement des photographies flatteuses, du moins au centre, et la profondeur de champ paraîtra augmentée. En effet, en se tenant trois fois trop loin, tout se passe comme si l'on tolérait une limite de netteté divisée par 3, donc 1/500 au lieu de 1/1500.
• À la distance orthoscopique, les bords de l'image sont nettement plus éloignés de l'œil que la zone centrale et vus très obliquement, ce qui diminue tout à fait normalement l'angle de vision pour les détails qui s'y trouvent. Ce double effet s'atténue très vite dès que la distance d'observation augmente, ce qui justifie la réputation qu'ont ces objectifs de déformer les images. On peut, bien sûr, détourner cet effet à son profit pour obtenir des photographies spectaculaires, mais dans ce cas, la notion de profondeur de champ perd toute signification.

Photo d'un bateau prise avec un objectif de 50 mm

Photo du même bateau prise avec un objectif de 17 mm

Tout comme pour les téléobjectifs, les très bons grand-angulaires sont des pièces d'optique très onéreuses. Le problème pour les opticiens est de trouver des formules optiques permettant de corriger en même temps toute une série d'aberrations, sans créer de vignetage et en conservant une ouverture raisonnable.