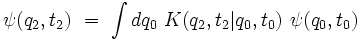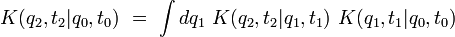Propagateur de l'équation de Schrödinger - Définition
La liste des auteurs de cet article est disponible ici.
Application au calcul d'une amplitude de transition
L'amplitude de transition pour que la particule passe d'état initial | ψ(t1) > à l'instant t1 vers un état  à l'instant t2 > t1 est donné par l'élément de matrice :
à l'instant t2 > t1 est donné par l'élément de matrice :
 |
En insérant deux fois la relation de fermeture, on obtient :
 |
c’est-à-dire :
|
|
On constate donc que la connaissance du propagateur permet de calculer n'importe quelle amplitude de transition quantique, au moins formellement.
Équation de Chapman-Kolmogorov
La fonction d'onde à un instant t2 > t1 est donnée par l'équation intégrale :
|
|
En introduisant dans cette équation la relation entre ψ(q1,t1) et ψ(q0,t0), on obtient :
|
|
qu'on peut écrire :
|
|
Mais comme on peut aussi écrire directement que :
|
|
On en déduit la formule fondamentale suivante :
|
|
Cette relation porte le nom d'équation de Chapman-Kolmogorov dans la théorie des processus stochastiques, dont le mouvement brownien est un cas particulier.
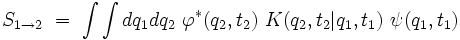
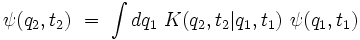
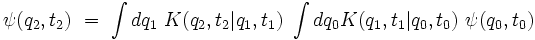
![\psi(q_2,t_2) \ = \ \int dq_0 \ \left[ \ \int dq_1 \ K(q_2,t_2|q_1,t_1) \ K(q_1,t_1|q_0,t_0) \ \right] \ \psi(q_0,t_0)](https://static.techno-science.net/illustration/Definitions/autres/8/81aafb2ad4d366083e338ef4fd721c8c_5b153f53fc46875881aad7672c3917ee.png)