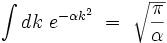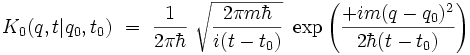Propagateur de l'équation de Schrödinger - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le terme propagateur a été introduit en physique par Feynman en 1948 pour sa formulation de la mécanique quantique en intégrales de chemin, une nouvelle approche de la quantification centrée sur le Lagrangien, contrairement à la procédure habituelle de quantification canonique fondée sur le Hamiltonien.
Le propagateur, outil mathématique très commode, sera rapidement identifié par Dyson comme n'étant rien d'autre qu'une fonction de Green. Cette remarque permettra à Dyson de faire en 1948 le lien manquant entre la formulation abstraite de l'électrodynamique quantique développée par Schwinger, et celle, basée sur des diagrammes, inventée indépendamment par Feynman.
Propagateur
Introduction
Considérons une particule non relativiste de masse m à une dimension, dont l'opérateur Hamiltonien s'écrit :
|
|
En représentation de Schrödinger, cette particule est décrite par le ket

|
|
Si l'on se donne à un instant initial t0 fixé une condition initiale

|
|
Projetons cette équation dans la représentation des positions :
|
|
et insérons la relation de fermeture dans le terme de droite :
|
|
il vient :
|
|
Compte-tenu du fait que
|
|
Définition
On définit le propagateur de l'équation de Schrödinger par :
 |
de telle sorte que la fonction d'onde évolue selon l'équation intégrale :
|
|
Remarque
Comme ψ(q,t) est une solution de l'équation de Schrödinger, le propagateur est aussi une solution de cette équation :
|
|
qui doit de plus vérifier la condition initiale :
|
|
Les mathématiciens parlent dans ce cas d'une solution élémentaire de l'équation de Schrödinger, les physiciens utilisant plutôt le nom de fonction de Green.
Expression du propagateur de la particule libre
Rappels sur la transformation de Fourier
On rappelle les relations :
Avec les notations de Dirac, et en utilisant la relation de fermeture sur les impulsions :
la seconde relation s'écrit :
On tire la formule suivante :
Expression du propagateur de la particule libre
Pour une particule libre sur la droite, l'opérateur Hamiltonien est indépendant de la position :
Le propagateur, qu'on note dans ce cas K0, s'écrit alors :
Insérons alors deux fois la relation de fermeture pour les impulsions dans la définition du propagateur :
Le ket | p0 > étant par définition un état propre de l'opérateur impulsion
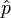
et l'élément de matrice devient :
Sachant que < p | p0 > = δ(p − p0), on obtient pour le propagateur :
Compte-tenu de la formule démontrée précédemment avec la transformée de Fourier, il vient :
qui se réécrit :
L'argument de l'exponentielle peut se réécrire comme suit :
Or le crochet est le début d'un carré parfait :
donc l'argument de l'exponentielle devient :
Le dernier terme étant indépendant de l'impulsion, il sort de l'intégrale et le propagateur s'écrit :
On fait un changement de variable sur les impulsions, les autres paramètres étant fixés :
ce qui donne :
Il subsiste une intégrale Gaussienne qui se calcule exactement :
On en déduit que :
d'où l'expression finale du propagateur libre :
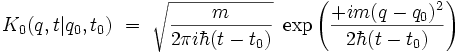
|
Remarque
Pour une particule libre dans un espace Euclidien à d dimensions, on pourrait démontrer de façon analogue que :

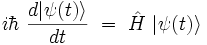


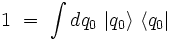


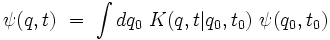


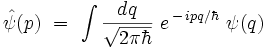
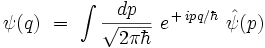



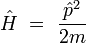





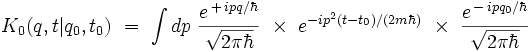
![K_0(q,t|q_0,t_0) \ = \ \int \frac{dp}{2 \pi \hbar} \ \exp \left[ \, \frac{i p (q-q_0)}{\hbar} \ - \ \frac{ip^2(t-t_0)}{2m\hbar} \, \right]](https://static.techno-science.net/illustration/Definitions/autres/9/9d6386a4a2d214e8d51ae6482b4d51ce_3acda15208629848b38abadaad47b9f7.png)
![\frac{i p (q-q_0)}{\hbar} \ - \ \frac{ip^2(t-t_0)}{2m\hbar} \ = \ - \ \frac{i (t-t_0)}{2m\hbar} \ \times \ \left[ \ p^2 \ - \ \frac{2mp(q-q_0)}{(t-t_0)} \ \right]](https://static.techno-science.net/illustration/Definitions/autres/d/dfdc547ef4de710bf73200e37acae5a7_5479ee80cfec9f5df523c54da0e05e6a.png)
![p^2 \ - \ \frac{2mp(q-q_0)}{(t-t_0)} \ = \ \left[ \ p \ - \ \frac{m(q-q_0)}{(t-t_0)} \ \right]^2 \ - \ \frac{m^2(q-q_0)^2}{(t-t_0)^2}](https://static.techno-science.net/illustration/Definitions/autres/c/c8c51d3438bfaf938dbb908060e74082_592bc5d2a62645aa95fa77ea75b9417e.png)
![- \ \frac{i (t-t_0)}{2m\hbar} \ \times \ \left[ \ \left( \ p \ - \ \frac{m(q-q_0)}{(t-t_0)} \ \right)^2 \ - \ \frac{m^2(q-q_0)^2}{(t-t_0)^2} \right]](https://static.techno-science.net/illustration/Definitions/autres/b/bdf22f9a51c6e3ba759e15607a881424_ecf7cadce2ee54fc34c86da8d9029bc9.png)
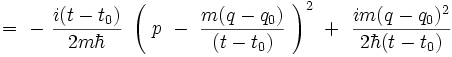
![K_0(q,t|q_0,t_0) \ = \ \exp \left( \frac{i m(q-q_0)^2}{2 \hbar (t-t_0)} \right) \ \times \ \int \frac{dp}{2 \pi \hbar} \ \exp \left[ \, - \ \frac{i (t-t_0)}{2m\hbar} \ \left( \ p \ - \ \frac{m(q-q_0)}{(t-t_0)} \ \right)^2 \, \right]](https://static.techno-science.net/illustration/Definitions/autres/7/7727affce85506a466eb065f0127ff17_ebe852df1b2f830649900fe006fea041.png)
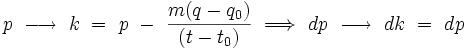
![K_0(q,t|q_0,t_0) \ = \ \frac{1}{2 \pi \hbar} \ \exp \left( \frac{i m(q-q_0)^2}{2 \hbar (t-t_0)} \right) \ \times \ \int dk \ \exp \left[ \, - \ \frac{i (t-t_0) k^2}{2m\hbar} \, \right]](https://static.techno-science.net/illustration/Definitions/autres/a/aa69fe9039b19a027b2fd84f12b4e91a_9611a5b536c99c3456d0fccb9ae9bd6d.png)