Racine d'un polynôme - Définition
La liste des auteurs de cet article est disponible ici.
Existence des racines
Soit P un polynôme à une indéterminée et à coefficients dans un corps commutatif K. Il existe toujours une extension L telle que le polynôme P soit scindé dans L, ce qui peut s'exprimer de la manière suivante :
Existence des racines — Il existe une unique plus petite extension L de K, à un isomorphisme près, telle que P se décompose de manière unique en un produit d'une constante de L et de n polynômes unitaires du premier degré, si n désigne le degré P. L'extension L est appelée corps de décomposition de P.
L'unicité de L signifie que si deux extensions L1 et L2 sont les plus petites au sens de l'inclusion, alors L2 est une copie de L1, c'est-à-dire qu'il existe un isomorphisme de corps entre L1 et L2. La démonstration est donnée dans l'article détaillé. Un polynôme unitaire est un polynôme dont le monôme de plus haut degré est de coefficient égal à 1. Chaque constante de ces polynômes unitaires du premier degré sont égales à l'opposé d'une racine du polynôme P. Si L est une extension telle que le polynôme P soit scindé, il est possible de factoriser tous les coefficients des monômes du premier degrés des différents facteurs de la décomposition et trouver ainsi la forme décrite dans la proposition précédente.
Cette proposition s'exprime aussi d'une manière équivalente, si les racines sont comptées avec leur ordre de multiplicité, c'est-à-dire si une racine d'ordre de multiplicité m est comptée m fois :
Existence des racines (bis) — Il existe une unique, à un isomorphisme près, plus petite extension L de K, telle que P contienne exactement autant de racines que le degré de P.
Le corps L est tel que le polynôme P est scindé, en revanche un autre polynôme à coefficients dans K n'est pas nécessairement scindé dans L. A fortiori, un polynôme à coefficients dans L n'est pas non plus nécessairement scindé dans L. On dit qu'un corps L est algébriquement clos si tout polynôme à coefficients dans L est scindé :
Existence d'une clôture algébrique — Soit K un corps commutatif, il existe un corps L algébriquement clos et contenant K.
Un exemple de corps algébriquement clos est C, résultat connu sous le nom de Théorème de d'Alembert-Gauss. Ainsi tout polynôme à coefficient dans Q, R ou C admet autant de racines que son degré dans C. Le corps C n'est pas le plus petit corps contenant Q et algébriquement clôt. Il en existe néanmoins un, appelé la clôture algébrique de Q, plus petit que tous les autres. La clôture algébrique de R est exactement égale à C.
Calcul des racines
On peut utiliser la méthode de Müller pour calculer les racines d'un polynôme. On interpôle le polynôme P par un polynôme de degré deux : a2x2 + b2x + c2 selon l'interpolation lagrangienne. On retrouve les coefficients en évaluant P en trois points (x0,x1,x2) :
Avec :
![f[u, v] = \frac{f(u) - f(v)}{u - v}](https://static.techno-science.net/illustration/Definitions/autres/2/25b104837121808658c27f555fec4888_8c169a6ac6c3a38ac01d46905bc14696.png)
Mais en utilisant ce polynôme d’approximation, le choix de la racine de ce polynôme est problématique. Müller eut alors l’idée d’utiliser le même polynôme, mais sous la forme : an(x − xn)2 + bn(x − xn) + cn avec xn qui va tendre vers la racine. Particularité de cet algorithme : xn peut-être un nombre complexe. Coefficients :
- an = P[xn − 2,xn − 1,xn]
-
![b_n = P[x_{n-1}, x_n] - a_n\times (x_{n-1} - x_n)](https://static.techno-science.net/illustration/Definitions/autres/e/e39e05413ca428ddb3ae535b73e2220d_135556dbbd5fd19375b6e3b8e976c609.png)
- cn = P(xn)
Cette méthode est autoconvergeante : le calcul de la racine va s'affiner petit à petit. On peut donc commencer avec x0 = − 1, x1 = 0 et x2 = 1 et n = 2. Tant que le polynôme ne s'annule pas en xn, on passe à l'itération n + 1 suivante avec :
-
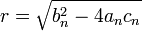
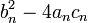
-
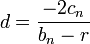
-
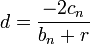
-
- xn + 1 = xn + d
Finalement, le zéro est xn.
![a_2 = \frac{P[x_0, x_1] - P[x_1, x_2]}{x0 - x2} = P[x_0, x_1, x_2]](https://static.techno-science.net/illustration/Definitions/autres/1/1b85365ab2c2981317d62b753d4625b1_79953c8d2cbed1a6afc5073c8b60ee50.png)
![b_2 = P[x_1, x_2] - a_2\times (x1 + x2)](https://static.techno-science.net/illustration/Definitions/autres/4/49e660ebd0a7dfe066021bd7edc4e0af_c5fa3c2b14cdfd4cea3b2bbe388bd9af.png)