Racine d'un polynôme - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définitions - Existence des racines - Calcul des racines

Introduction

En mathématiques, une racine α d'un polynôme à une indéterminée P(X) est une valeur α qui, si elle est substituée à l'indéterminée, donne une expression nulle. En ce sens, une racine du polynôme est une solution de l'équation polynomiale P(X) = 0. Par exemple, si P est le polynôme X² - 2, alors √2 et -√2 sont les racines de P. Le théorème de d'Alembert-Gauss indique que tout polynôme P non constant à coefficients dans les nombres complexes admet au moins une racine. Cela signifie qu'il existe toujours un nombre complexe α, racine de P, ou encore que P(α) = 0.

Le polynôme P possède des coefficients dans un ensemble de nombres qui ne contient pas nécessairement de racine. Ainsi, le polynôme exemple est à coefficients dans l'ensemble des nombres rationnels. Cela ne signifie pas qu'une racine du polynôme soit nécessairement dans le même ensemble. Le polynôme exemple possède des racines dans l'ensemble des nombres réels mais pas dans l'ensemble des nombres rationnels.

Par extension, le terme racine est aussi utilisé pour décrire une solution d'une équation, en général polynomiale. Par abus, certains appellent racine d'une fonction f, un zéro de la fonction f. Cet usage du mot racine est traité dans l'article Inconnue (mathématiques).

Le terme de racine se généralise à un polynôme en plusieurs indéterminées.

Définitions

Définition

On considère un polynôme P(X) à une indéterminée notée ici X, à coefficients dans un corps commutatif noté K. Un corps est un ensemble munis d'une addition et d'une multiplication. Il existe un élément neutre pour la multiplication, en général noté 1 et tout élément non nul est inversible. Des exemples de corps fréquemment utilisés sont Q, l'ensemble des rationnels, R celui des réels ou C celui des nombres complexes. En informatique, on utilise fréquemment les polynômes sur un corps fini à deux éléments, noté F₂. Dire que le corps est commutatif revient à dire que la multiplication l'est.

Une extension L d'un corps K est un corps contenant K, ainsi R et C sont des extensions de Q.

Définition de racine — Une racine α du polynôme P est un élément d'une extension L de K tel que, si l'on substitue à l'indéterminée X la valeur α, on obtient une expression nulle dans L.

Ainsi, le polynôme X² - 2, à coefficients dans Q, possède deux racines √2 et -√2, même si ces racines ne sont pas des éléments de Q. En effet, si l'on substitue √2 ou -√2 à X dans le polynôme, on trouve bien 0. Ces racines peuvent être vues comme des éléments de R ou de C.

Une question naturelle se pose, si L₁ et L₂ sont deux extensions de K contenant toutes les racines de P(X). Les racines, vues comme éléments de L₁ sont-elle équivalentes aux racines vues comme éléments de L₂ ? Cette équivalence existe, il existe toujours une autre extension L de K, appelé corps de décomposition de P(X), contenant toutes les racines de P(X). Cette extension est une copie d'un corps inclus dans L₁, de plus ce corps inclus dans L₁ est unique. Ces propriétés sont aussi vrai pour L₂. On peut ainsi identifier une partie de L₁ à une partie de L₂ à L. Dans l'exemple choisi, L est l'ensemble des nombres de la forme a + b.√2, où a et b sont des nombres rationnels. Cet ensemble L s'identifie à une partie de R et de C. Ainsi, les deux racines √2 et -√2, vues comme éléments de L de R ou de C peuvent être considérées comme identiques.

Étymologie : Le terme de racine provient des traductions en latin de Robert de Chester et de Gérard de Crémone du terme gizr. Le mot gizr signifie racine, il est traduit en latin par radix. Le terme gizr est utilisé par le mathématicien d'origine perse du VIII^e siècle Al-Khawarizmi, dans son traité Kitâb al-jabr wa al-muqâbala, qui traite pour la première fois de manière exhaustive, du calcul des racines réelles de l'équation du second degré.

Définition alternative

On utilise aussi une autre manière de définir les racines d'un polynômes, strictement identique à la définition précédente :

Définition alternative — Une racine α du polynôme P est un élément d'une extension L de K tel que le polynôme P, considéré comme à coefficients dans L, soit un multiple du polynôme X - α.

Cette définition indique que α est une racine de P si, et seulement si, il existe un polynôme Q, à coefficients dans L tel que P = (X - α)Q. Dans l'exemple choisi, l'égalité :

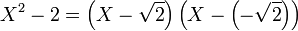
est une autre manière de remarquer que √2 et -√2 sont bien les deux racines du polynôme. L'équivalence des deux définitions est donnée dans l'article Polynôme formel.

Définitions connexes

Une racine de P peut être multiple, ce qui correspond à la définition suivante :

Racine multiple — Une racine α du polynôme P est dite multiple, d'ordre de multiplicité m, où m est un entier strictement supérieur à 1, s'il existe un polynôme Q, tel que P soit égal à (X - α)^mQ, et que Q ne s'annule pas en α.

Une définition caractérise une racine qui n'est pas multiple :

Racine simple — Une racine α du polynôme P est dite simple si elle n'est pas multiple. On dit que son ordre de multiplicité est égal à 1.

Dans le premier exemple cité, le polynôme X² - 2 s'exprime, dans l'ensemble des polynômes à coefficients réels, comme un produit de polynôme du premier degré, ce qui donne lieu à une définition :

Polynôme scindé — Soient L une extension de K et P un polynôme à coefficients dans K. Si P s'exprime comme le produits de polynômes du premier degré à coefficients dans L, on dit que le polynôme P est scindé dans L.