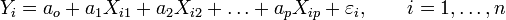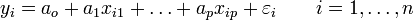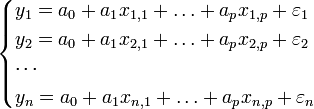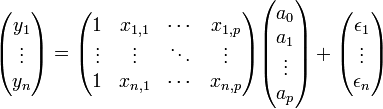Régression linéaire multiple - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Modèle théorique - Évaluation - La méthode des moindres carrés ordinaires - Régression de séries temporelles - Un exemple

Modèle théorique

La régression linéaire multiple est une généralisation, à p variables explicatives, de la régression linéaire simple.

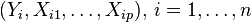
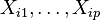
Nous sommes toujours dans le cadre de la régression mathématique : étant donné un échantillon $(Y_i, X_{i1}, \ldots, X_{ip}), \, i = 1, \ldots, n$ nous cherchons à expliquer, avec le plus de précision possible, les valeurs prises par $Y i$ , dite variable endogène, à partir d'une série de variables explicatives $X_{i1}, \ldots, X_{ip}$ . Le modèle théorique, formulé en termes de variables aléatoires, prend la forme

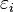
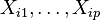
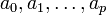
où $\varepsilon_i$ est l'erreur du modèle qui exprime, ou résume, l'information manquante dans l'explication linéaire des valeurs de $Y i$ à partir des $X_{i1}, \ldots, X_{ip}$ (problème de spécifications, variables non prises en compte, etc.). $a_0, a_1, \ldots, a_p$ sont les paramètres à estimer.

Exemple

Nous relevons 20 fois les paramètres suivants : la demande totale en électricité (ce sera notre $y i$ , i étant compris entre 1 et 20) la température extérieure (ce sera notre $x i 1$ ) l'heure à laquelle les données sont prises (ce sera notre $x i 2$ )

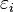
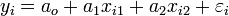
Faire une régression linéaire revient à déterminer les $a o$ , $a 1$ et $a 2$ et $\varepsilon_i$ tels que, quelle que soit la mesure prise, on ait : $y_i = a_o + a_{1} x_{i1} + a_{2} x_{i2} + \varepsilon_i$

Estimation

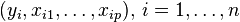
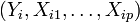
Lorsque nous disposons de n observations $(y_i, x_{i1}, \ldots, x_{ip}), \, i = 1, \ldots, n$ , qui sont des réalisations des variables aléatoires $(Y_i, X_{i1}, \ldots, X_{ip})$ , l'équation de régression s'écrit

La problématique reste la même que pour la régression simple :

estimer les paramètres $a i$ en exploitant les observations ;
évaluer la précision de ces estimateurs ;
mesurer le pouvoir explicatif du modèle ;
évaluer l'influence des variables dans le modèle :
- globalement (les p variables en bloc) et,
- individuellement (chaque variable) ;
évaluer la qualité du modèle lors de la prédiction (intervalle de prédiction) ;
détecter les observations qui peuvent influencer exagérément les résultats (points atypiques).

Notation matricielle

Nous pouvons adopter une écriture condensée qui rend la lecture et la manipulation de l'ensemble plus facile. Les équations suivantes

\begin{cases} y_1 = a_0 + a_1 x_{1,1} + \ldots + a_p x_{1,p} + \varepsilon_1\\ y_2 = a_0 + a_1 x_{2,1} + \ldots + a_p x_{2,p} + \varepsilon_2\\ \cdots\\ y_n = a_0 + a_1 x_{n,1} + \ldots + a_p x_{n,p} + \varepsilon_n \end{cases}

peuvent être résumées avec la notation matricielle

\begin{pmatrix} y_1 \\ \vdots\\ y_n \end{pmatrix} = \begin{pmatrix} 1 & x_{1,1} & \cdots & x_{1,p} \\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_{n,1} & \cdots & x_{n,p} \end{pmatrix} \begin{pmatrix} a_0\\ a_1\\ \vdots\\ a_p\\ \end{pmatrix} + \begin{pmatrix} \epsilon_1\\ \vdots\\ \epsilon_n\\ \end{pmatrix}

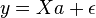
Soit de manière compacte: $y = Xa + \epsilon \,$

avec

y est de dimension (n, 1)
X est de dimension (n, p + 1)
a est de dimension (p+1, 1)
ε est de dimension (n, 1)
la première colonne sert à indiquer que nous procédons à une régression avec constante.

Hypothèses

Comme en régression simple, les hypothèses permettent de déterminer : les propriétés des estimateurs (biais, convergence) ; et leurs lois de distributions (pour les estimations par intervalle et les tests d'hypothèses).

Il existe principalement deux catégories d'hypothèses :

Hypothèses stochastiques

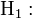
$\mathrm{H_{1}: }\,$ Les X_j sont aléatoires, j = 1, …, p ;
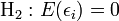
$\mathrm{H_{2}: } \ E(\epsilon_i) = 0 \,$ Le modèle est bien spécifié en moyenne ;
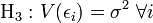
$\mathrm{H_{3}: } \ V(\epsilon_i) = \sigma^2 \ \forall{i} \,$ Homoscedasticité (en) des erreurs (variance constante)
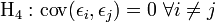
$\mathrm{H_{4}: } \ \mathrm{cov}(\epsilon_i, \epsilon_j) = 0 \ \forall{i \neq j} \,$ Pas d'autocorrélation des erreurs.
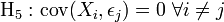
$\mathrm{H_{5}: } \ \mathrm{cov}(X_i, \epsilon_j) = 0 \ \forall{i \neq j} \,$ Les erreurs sont linéairement indépendantes des variables exogènes.
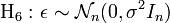
$\mathrm{H_{6}: } \ \epsilon \sim \mathcal{N}_n(0,\sigma^2 I_n) \,$ Les erreurs suivent une loi normale multidimensionnelle ( $H 6$ implique les hypothèses $H 2$ , $H 3$ et $H 4$ la réciproque étant fausse car les 3 hypothèses réunies n'impliquent pas que $\ \epsilon \$ soit un vecteur gaussien).

Hypothèses structurelles

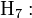
$\mathrm{H_{7}: }\,$ absence de colinéarité entre les variables explicatives, i.e. X 'X est régulière, det(X 'X) ≠ 0 et (X 'X)^-1 existe (remarque : c'est équivalent à rang(X) = rang(X 'X) = p + 1) ;
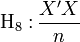
$\mathrm{H_{8}: }\, \frac{X'X}{n}$ tend vers une matrice finie non singulière lorsque n → +∞ ;
$\mathrm{H_{9}: } \ n >p+1\,$ Le nombre d'observations est supérieur au nombre de variables + 1 (la constante). S'il y avait égalité, le nombre d'équations serait égal au nombre d'inconnues a_j, la droite de régression passerait par tous les points, nous serions face à un problème d'interpolation linéaire (voir Interpolation numérique).

Écriture matricielle de l'hypothèse $H 6$

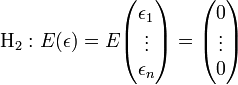
$\mathrm{H_{2}:} \ E(\epsilon) = E \begin{pmatrix} \epsilon_1\\ \vdots\\ \epsilon_n \end{pmatrix} = \begin{pmatrix} 0\\ \vdots\\ 0 \end{pmatrix}$

Sous l'hypothèse d'homoscedasticité et d'absence d'auto-corrélation, la matrice de variance-covariance du vecteur des erreurs peut s'écrire:

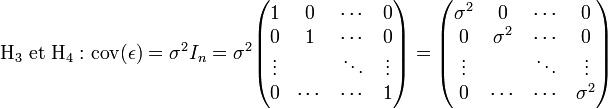
$\mathrm{H_{3} \ \mbox{et} \ H_{4}:}\ \mathrm{cov}(\epsilon) = \sigma ^2 I_n = \sigma ^2 \begin{pmatrix} 1 & 0 & \cdots &0 \\ 0 & 1 & \cdots &0 \\ \vdots & & \ddots& \vdots \\ 0 & \cdots &\cdots&1 \end{pmatrix} = \begin{pmatrix} \sigma^2 & 0 & \cdots &0 \\ 0 & \sigma^2 & \cdots &0 \\ \vdots & & \ddots& \vdots \\ 0 & \cdots &\cdots&\sigma ^2 \end{pmatrix}$

Régresseurs stochastiques

Dans certains cas, l'hypothèse (H1) est intenable : les régresseurs X sont supposés aléatoires. Mais dans ce cas, on suppose que X est aléatoire mais est indépendant de l'aléa $\varepsilon$ . On remplace alors l'hypothèse (H2) par une hypothèse sur l'espérance conditionnelle:

De même, il faudrait changer en conséquence les hypothèses (H3), (H4) et aussi (H5).

Évaluation

- Modèle théorique - Évaluation - La méthode des moindres carrés ordinaires - Régression de séries temporelles - Un exemple

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔

A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟

Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭

Une méthode simple pour améliorer les performances en mathématiques 🧮

Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡

Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬

Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭

Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘

Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉

Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠

Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥

Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊

L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭

Cet édulcorant tue les superbactéries résistantes 🍬

Les neutrinos, la clé de la gravité quantique ? 👀

En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋

Que sont ces spaghettis au cœur de notre galaxie ? 🔭

Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯

Les nanoplastiques, l'amiante du 21ème siècle ? 🔬

Compétition cellulaire: des forces sculptent nos tissus 🛠️

Le climat en Europe et au États-Unis pourrait changer bien plus radicalement que supposé 🌍

Découverte: ce dinosaure avait des poches d'air dans les os 🦴

La vie sur Titan, si elle existe, ressemblerait à quoi ? 🪐

Magnétisme et biologie s'allient contre le cancer 🧲

WR 104: on en sait plus sur cette "étoile de la mort" qui menace la Terre ☄️

Découverte: des bactéries respiraient de l'oxygène 1 milliard d'années avant la Grande Oxydation 🫧

Découverte d'un nouveau type de vent solaire rapide ☀️

Les dinosaures n'étaient pas en déclin avant l'astéroïde 🦖

Ce robot-cheval est véritablement tout-terrain 🐎

Comment un mauvais sommeil peut endommager votre cerveau ? 🧠

Découverte de microbes cachés qui purifient l'eau sans que nous le sachions 💧

Bonne nouvelle pour les enfants de la Lune 🌙

Du CO2 détecté dans l'atmosphère d'une exoplanète proche 🔭

Le café et le thé impactent le cancer, mais dans quel sens ? ☕

Une IA révèle des bulles cosmiques dans notre galaxie 🫧

Lorsque l'alcool stimule ses phéromones sexuelles et rend plus séduisant 🍷

Page générée en 0.104 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise