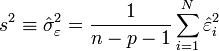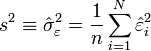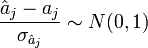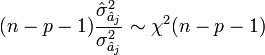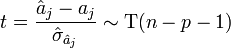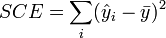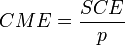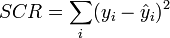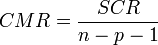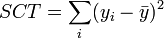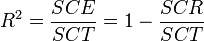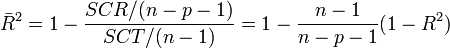Régression linéaire multiple - Définition
La liste des auteurs de cet article est disponible ici.
Évaluation
Pour réaliser les estimations par intervalle et les tests d'hypothèses, la démarche est presque toujours la même en statistique paramétrique :
- définir l'estimateur (â dans notre cas) ;
- calculer son espérance mathématique (ici E(â ) = a) ;
- calculer sa variance (ou sa matrice de variance co-variance) et produire son estimation ;
- et enfin déterminer sa loi de distribution (en général et sous l'hypothèse nulle des tests).
Matrice de variance-covariance de â
La matrice de variance-covariance des coefficients est importante car elle renseigne sur la variance de chaque coefficient estimé, et permet de faire des tests d'hypothèse, notamment de voir si chaque coefficient est significativement différent de zéro. Elle est définie par :
![\operatorname{Var}(\hat a)\equiv \Sigma = \operatorname{E}[(\hat a- a)(\hat a- a)']](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/98f0798443d48ea38c2eeada6eac8629_ba04477787c2aa33b2324688dc85f2ca.png)
Sous les hypothèses d'espérance nulle, d'absence d'autocorrélation et d'hétéroscédasticité des résidus (H1 à H5), on a:
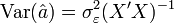
en récrivant:
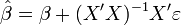
![\begin{align} \operatorname{Var}[\hat \beta] &= \operatorname{Var}\left[(X'X)^{-1}X'\varepsilon \right ]\\ &=(X'X)^{-1}X'\operatorname{Var}[\varepsilon] X(X'X)^{-1}\\ &=(X'X)^{-1}X'\sigma^2_{\varepsilon}I X(X'X)^{-1}\qquad \text{ sous } H_3 \text{ et } H_4\\ &=\sigma^2_{\varepsilon}(X'X)^{-1}X'X(X'X)^{-1}\\ &=\sigma^2_{\varepsilon}(X'X)^{-1} \end{align}](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/09f73b4f4959f97a82d8f1eb588b81cc_ee06f046b23517f99beee4f46e20c4d8.png)
Cette formule ne s'applique cependant que dans le cas où les résidus sont homoscédastiques et sans auto-corrélation, ce qui permet d'écrire la matrice des erreurs comme:
![\textrm{Cov}[\varepsilon] = \sigma^2 I_{n} \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/5/5d54b9905389d754bd36b55bbae4dadf_3d6f4d5df2337509542558fe422042d0.png)
S'il y a de l'hétéroscédasticité ou de l'auto-corrélation, et donc
![\textrm{Cov}[\varepsilon] \neq \sigma^2 I_{n}](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4fb7cb0c423a1b4eb09b12e8be7dd7ba_67e36bf51c295ad90c7f6ba6acea7842.png)
- Matrice de variance-covariance de White (ou Eicker-White (1967, 1980)), consistante en cas d'hétéroscédasticité (en anglais HC Heteroskedasticity Consistent).
- Matrice de variance-covariance de Newey-West (1987), consistante en cas d'hétéroscédasticité et d'auto-corrélation (en anglais HAC Heteroskedasticity and Autocorrelation Consistent).
Ces deux estimateurs sont disponible pour le logiciel libre de statistique R dans le paquet externe "sandwich".
Estimation de la variance du résidu
Pour la variance du résidu
![\sigma_{\varepsilon}^{2}\equiv \operatorname{Var}[\varepsilon]](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/707adaf7ebd3ecabcfebe90406facf5d_4e3b42f432918153416ba515ba624166.png)
Les
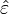
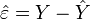
On remarque deux choses par rapport à l'estimateur classique de la variance:
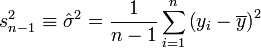
- on n'inclut pas l'espérance des résidus, car celle-ci est supposée être de zéro (selon H2). Surtout, les résidus du modèle ont exactement une moyenne de zéro lorsqu'une constante est introduite dans le modèle.
- La somme des carré est divisé par n - p - 1 = n - (p + 1) et non par n-1. En fait, n-p-1 correspond aux degrés de liberté du modèle (le nombre d'observations moins le nombre de coefficients à estimer). on remarque effectivement que
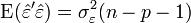
Il existe également un autre estimateur, obtenu par la méthode du maximum de vraisemblance, qui est cependant biaisé:
Estimation de la matrice de variance-covariance de â
Il suffit de remplacer la variance théorique des résidus,
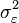
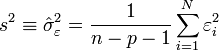
L'estimateur de la matrice de variance-covariance des résidus devient:
La variance estimée
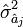
Étude des coefficients
Après avoir obtenu l'estimateur, son espérance et une estimation de sa variance, il ne reste plus qu'à calculer sa loi de distribution pour produire une estimation par intervalle et réaliser des tests d'hypothèses.
Distribution
En partant de l'hypothèse
-
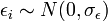
nous pouvons montrer
Le rapport d'une loi normale et de la racine carrée d'une loi du χ² normalisée par ses degrés de liberté aboutit à une loi de Student. Nous en déduisons donc la statistique :
elle suit une loi de Student à (n - p - 1) degrés de liberté.
Intervalle de confiance et tests d'hypothèses
À partir de ces informations, il est possible de calculer les intervalles de confiance des estimations des coefficients.
Il est également possible de procéder à des tests d'hypothèses, notamment les tests d'hypothèses de conformité à un standard. Parmi les différents tests possibles, le test de nullité du coefficient (H0 : a j = 0, contre H1 : a j ≠ 0) tient un rôle particulier : il permet de déterminer si la variable x j joue un rôle significatif dans le modèle. Il faut néanmoins être prudent quant à ce test. L'acceptation de l'hypothèse nulle peut effectivement indiquer une absence de corrélation entre la variable incriminée et la variable endogène ; mais il peut également résulter de la forte corrélation de x j avec une autre variable exogène, son rôle est masqué dans ce cas, laissant à croire une absence d'explication de la part de la variable.
Evaluation globale de la régression — Tableau d'analyse de variance
Tableau d'analyse de variance et coefficient de détermination
L'évaluation globale de la pertinence du modèle de prédiction s'appuie sur l'équation d'analyse de variance SCT = SCE + SCR, où
- SCT, somme des carrés totaux, traduit la variabilité totale de l'endogène ;
- SCE, somme des carrés expliqués, traduit la variabilité expliquée par le modèle ;
- SCR, somme des carrés résiduels correspond à la variabilité non-expliquée par le modèle.
Toutes ces informations sont résumées dans un tableau, le tableau d'analyse de variance.
| Source de variation | Somme des carrés | Degrés de liberté | Carrés moyens |
|---|---|---|---|
| Expliquée |
| p |
|
| Résiduelle |
| n - p - 1 |
|
| Totale |
| n - 1 |
Dans le meilleur des cas, SCR = 0, le modèle arrive à prédire exactement toutes les valeurs de y à partir des valeurs des x j. Dans le pire des cas, SCE = 0, le meilleur prédicteur de y est sa moyenne
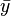
Un indicateur spécifique permet de traduire la variance expliquée par le modèle, il s'agit du coefficient de détermination. Sa formule est la suivante :
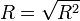
Dans une régression avec constante, nous avons forcément
- 0 ≤ R ² ≤ 1.
Enfin, si le R ² est certes un indicateur pertinent, il présente un défaut parfois ennuyeux, il a tendance à mécaniquement augmenter à mesure que l'on ajoute des variables dans le modèle. De ce fait, il est inopérant si l'on veut comparer des modèle comportant un nombre différent de variables. Il est conseillé dans ce cas d'utiliser le coefficient de détermination ajusté qui est corrigé des degrés de libertés :
Significativité globale du modèle
Le R ² est un indicateur simple, on comprend aisément que plus il s'approche de la valeur 1, plus le modèle est intéressant. En revanche, il ne permet pas de savoir si le modèle est statistiquement pertinent pour expliquer les valeurs de y.
Nous devons nous tourner vers les tests d'hypothèses pour vérifier si la liaison mise en évidence avec la régression n'est pas un simple artefact.
La formulation du test d'hypothèse qui permet d'évaluer globalement le modèle est la suivante :
- H0 : a1 = a2 = … = ap = 0 ;
- H1 : un des coefficients au moins est non nul.
La statistique dédiée à ce test s'appuie (parmi les différentes formulations possibles) sur le R ², il s'écrit :
-
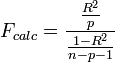
et suit une loi de Fisher à (p, n - p - 1) degrés de liberté.
La région critique du test est donc : rejet de H0 si et seulement si Fcalc > F1 - α(p, n - p - 1), où α est le risque de première espèce.
Une autre manière de lire le test est de comparer la p-value (probabilité critique du test) avec α : si elle est inférieure, l'hypothèse nulle est rejetée.
