Relation binaire - Définition

Relation fonctionnelle

Lorsque, pour tout élément x de E, x n’est en relation qu’avec 0 ou 1 élément y de F, on dit que la relation est fonctionnelle. C’est un cas particulier de fonction. En langage formel, la propriété précédente s’écrit :

Pour plus de précisions, voir l'article « Fonction mathématique ».

Exemple important :

La diagonale de E est définie par :

.

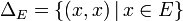
C’est le graphe de la relation d’égalité sur E, notée « =_E », ou « = » en l’absence d’ambiguïté sur l’ensemble concerné.

Cette relation est aussi une fonction, l’identité de E, notée « Id_E ».

Nombre de relations binaires sur des ensembles finis

Considérons un ensemble E fini de cardinal n et un ensemble F fini de cardinal p. Il y a autant de relations binaires de E sur F que d’applications de E×F dans { 0 , 1 } , ce qui donne 2 ^np relations.

En particulier, si E = F , on trouve relations binaires sur E, dont

• relations réflexives
• relations symétriques
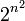
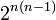
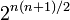
• Pour le nombre de relations transitives, il n’y a toujours pas actuellement de formule « fermée »

Le nombre de relations d’équivalence est égal au nombre de partitions d’un ensemble, c’est-à-dire le nombre de Bell.

Exemples

• La relation d’appartenance sur  ;
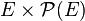
• la relation d’inclusion sur (relation d'ordre) ;
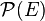
• la relation inférieur ou supérieur sur (relation d'ordre) ;
• la relation « est un diviseur de » sur (relation d'ordre) ;
• la relation d’égalité (congruencielle ou non) sur E (relation d'équivalence).

Bibliographie

• Nicolas Bourbaki, Eléments de mathématique. Théorie des ensembles,
• Paul R. Halmos, Introduction à la théorie des ensembles
• Yiannis Moschovakis, Notes on Set Theory