Introduction

Une relation ternaire interne dans un ensemble associe des éléments de cet ensemble à des couples formés d’éléments de ce même ensemble.

Définitions

Formellement, une relation ternaire interne est une correspondance dont l’ensemble de départ est le carré cartésien de l’ensemble d’arrivée.

En d’autres termes, une relation ternaire interne dans un ensemble E est la somme disjointe de trois ensembles :

• un ensemble de départ, E×E ;
• un ensemble d’arrivée, E ;
• et un graphe G, inclus dans E ³, donc formé de triplets d’éléments de E.

Si x, y et z sont trois éléments de E , nous pouvons écrire que z est image par du couple ( x , y ) de plusieurs manières :

• ( x , y , z ) ∈ G   (notation ensembliste)

• ( x , y , z )   (notation relationnelle postfixée)

• ( x , y , z )   (notation relationnelle préfixée)

• ( x , y ) z   (notation relationnelle infixée)

Nous utiliserons dans la suite cette dernière notation.

Cas particuliers :

• Une opération interne est une relation ternaire interne qui est aussi une fonction.

• Une loi de composition interne est une relation ternaire interne qui est aussi une application.

Exemples

• La relation d'équidistance dans un espace métrique, c'est-à-dire muni d'une distance d :

Un point A est équidistant de deux points B et C ssi d ( A , B ) = d ( A , C )

Ce n'est ni une opération, ni une loi de composition interne.

• L' exponentiation Exp définie par :   [ ( x , y ) Exp z ] ⇔ [ z = x ^y ]  

C'est une opération interne dans , à condition de donner un sens unique à x ^y quand il y a ambiguïté; ce n'est pas une loi interne dans  : par exemple, ( - 1 ) ^{1 / 2} n'a pas de sens dans .

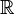
• La différence de deux ensembles Diff :   [ ( A , B ) Diff C ] ⇔ [ C = A \ B ] .

C'est une loi interne dans l'univers des ensembles, ou dans l'ensemble des parties d'un ensemble.

• Parmi les êtres humains, la relation « sont respectivement père et mère de » n'est ni une opération, ni une loi interne : un couple peut être sans enfants ou en avoir plusieurs.

• Les quatre « opérations » de notre enfance (addition, soustraction, multiplication et division) sont bien des opérations car leur résultat, quand il est défini, l'est toujours sans ambiguïté.

Relation ternaire opposée

Définition et exemples

Soit un ensemble E muni d'une relation ternaire interne .

La relation ternaire opposée à est la relation ternaire interne notée « -  » , et définie par :

Par exemple, la relation opposée à l' exponentiation Exp définie par :   [ ( x , y ) Exp z ] ⇔ [ z = x ^y ]   est la relation z = y ^x .

Un autre exemple est la différence de deux ensembles Diff :   [ ( A , B ) Diff C ] ⇔ [ C = A \ B ] .
Sa relation opposée est définie par [ ( A , B ) (-Diff) C ] ⇔ [ C = B \ A ].

Ou encore, parmi les êtres humains, la relation « sont respectivement père et mère de » a pour opposée la relation « sont respectivement mère et père de ».

Propriétés

• Chaque relation ternaire interne a une relation opposée et une seule.
• Toute relation ternaire est l'opposée de son opposée.
• L'opposée d'une relation ternaire est une opération si et seulement si cette relation est une opération.
• L'opposée d'une relation ternaire est une loi de composition si et seulement si cette relation est une loi de composition.
• Une relation ternaire se confond avec son opposée si et seulement si elle est commutative.