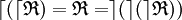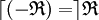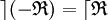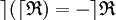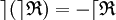Relation ternaire interne - Définition
La liste des auteurs de cet article est disponible ici.
Relations ternaires inverses
Présentation
Inverser une relation, c'est en quelque sorte en "inverser" les effets : par exemple, inverser une addition, où on a ajouté quelque chose, c'est retrancher de la somme ce qui a été ajouté, donc effectuer une soustraction. Il s'agit donc essentiellement de changer l'ordre des termes impliqués dans la relation.
De manière plus précise, inverser une relation, c'est permuter les composantes des n-uplets de son graphe, de la même manière pour tous les n-uplets, de sorte que les dernières composantes (les images), en deviennent les premières composantes.
Pour une relation binaire, dont les éléments du graphe sont des couples, cela revient à permuter les deux composantes de chacun de ces couples, c'est-à-dire à remplacer chaque couple par son réciproque; en résumé, la relation inverse d'une relation binaire n'est autre que sa relation réciproque.
Pour une relation ternaire, dont les éléments du graphe sont des triplets, inverser cette relation revient à permuter les composantes de ces triplets de sorte que la dernière composante devienne la première. Il reste deux façons de disposer les deux autres composantes, d'où a priori deux relations inverses. On appellera l'une relation inverse à gauche et l'autre relation inverse à droite.
Pour une relation n-aire, on dénombre ainsi (n - 1)! relations inverses a priori distinctes. On peut remarquer que toutes ces relations inverses sont de même arité intrinsèque que la relation qui leur a donné naissance.
Définitions et exemples
Soit un ensemble E muni d'une relation ternaire interne

La relation ternaire inverse à gauche ( ou RTIG) de la relation

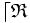
La relation ternaire inverse à droite ( ou RTID) de la relation

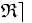
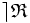
Pour clarifier ces notions reprenons l'exemple de l'exponentiation Exp.
- Sa RTIG est définie par : z = x 1/y ; autrement dit, c'est la racine y-ième de x;
- Sa RTID est définie par : z = log y x ; autrement dit, c'est le logarithme en base y de x.
Si

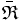
Exemples :
- la soustraction est la RTI de l'addition;
- la division est la RTI de la multiplication;
Ces exemples montrent qu'en général les RTI ne sont pas commutatives; sauf exception, elles n'ont donc pas elles-mêmes de RTI, seulement une RTIG et une RTID distinctes, la RTIG n'étant autre que la relation ternaire initiale, et la RTID l'opposée de la RTI.
Ainsi, la soustraction, non commutative, a pour RTIG l'addition et pour RTID la relation opposée à la soustraction. Cette dernière, par ailleurs, a pour RTID l'addition et pour RTIG la soustraction.
Propriétés
- Toute relation ternaire interne est la RTIG de sa RTIG, et la RTID de la RTID de sa RTID.
- La RTIG de l'opposée d'une relation ternaire est la RTID de cette dernière.
- La RTID de l'opposée d'une relation ternaire est la RTIG de cette dernière.
- La RTID de la RTIG d'une relation ternaire interne est la relation opposée à sa RTID.
- La RTID de la RTID d'une relation ternaire interne est la relation opposée à sa RTIG.
Dans les propriétés précédentes, des symétries apparaissent. Plus précisément, il est possible d'importer sur l'ensemble
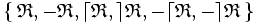

-

-

- Si

- Si

-

-

-

- Si

-

Exemples :
- (
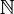
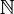
- de même, (


- (
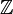
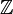
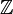
- de même, (


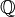
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \lceil \mathfrak{R} \, z ] \Leftrightarrow [ ( z , y ) \mathfrak{R} \, x ] \,](https://static.techno-science.net/illustration/Definitions/autres/2/2f55c9f753ba5ccc9a45a2bdf1279405_e920f8ad41cb38473fb820d7830a49ed.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \mathfrak{R} \rceil \, z ] \Leftrightarrow [ ( y , z ) \mathfrak{R} \, x ] \,](https://static.techno-science.net/illustration/Definitions/autres/7/74313d885ba31f7bd8bc08922c4ba37d_79d8d8ba15685404a3708b85f81ae1f8.png)