Relation ternaire interne - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Propriétés
Soit un ensemble E muni d’une relation ternaire interne

- Les propriétés suivantes s’appliquent évidemment aussi aux lois de composition internes, mais sous une forme simplifiée par l'emploi d'une notation fonctionnelle (z = f ( x, y ) ou z = x

- Attention : un couple peut très bien avoir plusieurs images par

- La liste de propriétés qui suit n’est pas exhaustive.
Existence d’éléments remarquables
-


- ou :
-
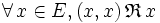
-


- ou :
-
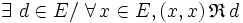
-


- ou :
-
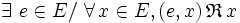
-


- ou :
-
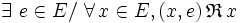
-

-


- ou :
-
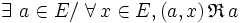
-


- ou :
-
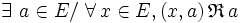
-

-

-

-

-

-

-

Régularité et propriétés apparentées
-


- ou :
-
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( x , y ) \mathfrak{R} \, t ] \Rightarrow [ z = y ] \,](https://static.techno-science.net/illustration/Definitions/autres/5/549f28404efae22a121c59b8bbce5754_fdb4e638d59969bf29cf55ae32fde48b.png)
-


- ou :
-
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( y , z ) \mathfrak{R} \, t ] \Rightarrow [ x = y ] \,](https://static.techno-science.net/illustration/Definitions/autres/0/03287cd94ae9ea382465cbba1b588fae_3e4e0c310f3d2e5a6634132075e5170e.png)
-

-


- ou :
-
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( y , x ) \mathfrak{R} \, t ] \Rightarrow [ z = y ] \,](https://static.techno-science.net/illustration/Definitions/autres/7/7b8e06ab3a08249344708d75e66aabf3_bba032b92809e634cf0df8c64b4abfe5.png)
Associativité et propriétés analogues
-

-

-

Autres propriétés
-


- ou :
-
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \mathfrak{R} \, z ] \Rightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](https://static.techno-science.net/illustration/Definitions/autres/3/38f24df8c6644fc316deef9c9a46eecb_d7c3c74b9e868fce2d556df5e695246c.png)
- Remarque : toute relation ternaire interne commutative est aussi associative des puissances.
Exemples
- la relation d'équidistance est commutative, dévolutive et idempotente;
- l'exponentiation est unifère à droite, mais pas à gauche, d'élément neutre 1; elle est absorbante à gauche, mais pas à droite, d'élément absorbant 1; elle est régulière à droite, mais pas à gauche;
- la relation "sont respectivement père et mère de" est régulière;
- la relation de concaténation des mots est associative, unifère d'élément neutre le mot vide "", et régulière;
![\forall ( u , v , w , x , y , z ) \in E^{\, 6} , [ ( x , y ) \mathfrak{R} \, u \wedge ( u , z ) \mathfrak{R} \, w \wedge ( y , z ) \mathfrak{R} \, v ] \Rightarrow [ ( x , v ) \mathfrak{R} \, w ] \,](https://static.techno-science.net/illustration/Definitions/autres/9/940aee35b1f55538fe40ca42ff68d6ff_0c1b4645ac15809c37a0d2a416d2b0ef.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , x ) \mathfrak{R} \, y \wedge ( x , y ) \mathfrak{R} \, z ] \Rightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](https://static.techno-science.net/illustration/Definitions/autres/5/5c428cff4b1bfe141f5d15654aea89f1_8cd618d52072c0c017a010d7275983cd.png)
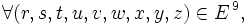
![[ ( x , y ) \mathfrak{R} \, z \wedge ( u , v ) \mathfrak{R} \, w \wedge ( x , u ) \mathfrak{R} \, r \wedge ( y , v ) \mathfrak{R} \, s \wedge ( z , w ) \mathfrak{R} \, t ] \Rightarrow [ ( r , s ) \mathfrak{R} \, t ] \,](https://static.techno-science.net/illustration/Definitions/autres/b/bc7737d69c6da100dc4200b465b62d96_49aebbcdf95c23a7b92d5d1ffc463d11.png)

















































