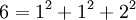Représentations du groupe symétrique d'indice trois - Définition

Représentation induite

Représentation induite par Z/3Z

Il existe une autre méthode pour construire une représentation, il suffit de considérer une représentation d'un sous-groupe et de construire la représentation induite. C'est l'approche utilisée dans ce paragraphe pour déterminer l'unique représentation irréductible fidèle de S₃.

Considérons H le sous groupe {1, c₁, c₂), E un espace vectoriel complexe de base f₁, et (E, α) la représentation de H, par exemple de caractère (1, j, j²). La théorie assure l'existence d'une unique représentation de S₃ (F, β) induite par α. Soit e₂ l'image de e₁ par β(t₁), comme t₁ n'est pas élément du groupe H, cet élément n'est pas inclus dans E. Comme S₃/H est d'ordre deux, F est de dimension le double de celle de E, donc de dimension deux. Ceci démontre que (e₁, e₂) est une base de F. Il ne reste plus qu'à déterminer l'image de cette base par la représentation β :

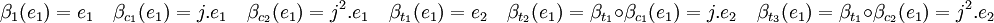
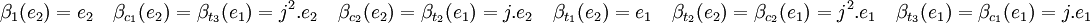
On en déduit la représentation matricielle B_x où x est un élément de S₃ de β :

Son caractère est égal à celui de θ, β et θ sont deux de représentations isomorphes. On retrouve, de manière plus simple, l'unique représentation irréductible de degré deux.

Formule de Frobenius

La formule de réciprocité de Frobenius permet de déterminer la nature de la représentation induite avant même de réaliser sa construction. Elle donne le produit scalaire de deux caractères dans S₃ en fonction du produit scalaire dans H :

Ici, Ind signifie le caractère de la représentation induite et Res signifie le caractère de la restriction à H.

Si K désigne le sous-groupe {1, t₁} et γ la représentation qui associe -1 à t₁, il est possible de déterminer a priori quel est la nature de γ :

La représentation de S₃ induite par la représentation non triviale de K est donc le produit direct des représentations θ et σ.

Caractère

Orthogonalité

Le caractère d'une représentation correspond à la fonction du groupe dans le corps qui à un élément s associe la trace de sa représentation. Dans les paragraphes précédents, cinq représentations ont été explicitées, la représentation régulière ρ, la triviale t, celle associée à la signature σ, celle associée à φ de degré quatre et enfin celle de θ de degré deux.

Si, à chaque valeur du groupe, on associe son caractère, on obtient le tableau suivant:

Car. de S3 1 t1 t2 t3 c1 c2 ρ 6 0 0 0 0 0 σ 1 -1 -1 -1 1 1 t 1 1 1 1 1 1 φ 4 0 0 0 -2 -2 θ 2 0 0 0 -1 -1

Les caractères sont associés à un produit hermitien. Si χ₁ et χ₂ sont deux caractères et si x^* désigne le nombre complexe conjugué de x, alors leur produit est le suivant :

Un caractère est irréductible si et seulement si sa norme, associé au produit scalaire est égale à un. Il est donc simple de vérifier que φ n'est pas une représentation irréductible, mais que θ l'est :

Deux représentations irréductibles sont orthogonales, il est simple de vérifier ce fait dans l'exemple S₃ :

Fonction centrale

Dans le cas de S₃ les caractères utilisés ici sont tous constants sur les classes de conjugaison. Cette propriété est générale à tous les groupes et toutes les représentations. Une fonction centrale est une application définie dans un groupe et constante sur chaque classe de conjugaison.

Les représentations irréductibles possèdent une autre propriété, il en existe autant que de classes de conjugaison. Dans le cas de S₃, il existe exactement trois classes de conjugaisons, celle de l'unité, celle des transpositions t et celle des cycles d'ordre trois c. Il existe de même trois représentations irréductibles, la triviale t, celle associée à la signature σ et celle de degré deux fidèle (c'est-à-dire injective) θ. Pour cette raison, les tableaux représentant les caractères des représentation d'un groupe sont des tableaux carrés, ne contenant que les représentations irréductibles, car les autres s'en déduisent par produit direct et définis sur les classes de conjugaison. On obtient pour le groupe S₃ le tableau suivant :

Car. irr. 1 c t t 1 1 1 σ 1 1 -1 θ 2 -1 0

La famille des caractères irréductibles est une famille libre car orthogonale, elle est génératrice car de cardinal la dimension de l'espace, c'est donc une base orthonormale des fonctions centrales. Cette propriété permet, à l'aide d'un caractère de déterminer la nature de la représentation à un isomorphisme près. Si χ est le caractère d'une représentation r et χ_i le caractère d'une représentation irréductible i, le produit hermitien <χ_r | χ_i> indique le nombre de copies de la représentation i présente dans r. Une opération de même nature que la Transformée de Fourier permet alors de déterminer toute représentation une fois les représentations irréductibles et leurs caractères connus. On vérifie par exemple que :

En conséquence, la représentation régulière contient une copie de la représentation triviale, une de la représentation signature et deux de la représentation θ, l'unique représentation de degré deux.

Dans le cas général, si h désigne le nombre de classe de conjugaison, d_i pour i compris entre 1 et h (qui est aussi le nombre de représentations irréductibles) le degré de la i-ième représentation irréductible et g l'ordre du groupe on dispose de la formule :

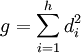
Ce qui, dans le cas particulier du groupe S₃, donne l'égalité suivante :