Représentation régulière - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et plus précisément en théorie des groupes, la représentation régulière est une représentation d'un groupe fini.
Soient G un groupe fini d'ordre g, K un corps, V un K espace vectoriel de dimension g et (es) une base de V indexée par G.
Soit ρ le morphisme de groupe de G dans le groupe linéaire GL(V), qui à un élément u de G associe l'automorphisme ρu de V défini comme suit sur la base de V : l'image du vecteur es par ρu est égal au vecteur eu.s.
Alors la représentation (V, ρ) est appelée représentation régulière de G.
Ce concept possède des propriétés importantes. Par exemple, toute représentation irréductible est isomorphe à une sous-représentation de la représentation régulière.
Définition
Soit G un groupe fini d'ordre g. Le groupe G opère par action de groupe (cf l'article associé) sur lui-même par la translation à gauche (resp. droite). Ce premier morphisme de G dans le groupe symétrique Sg montre que G est isomorphe à un sous-groupe de Sg. Ce résultat est connu sous le nom de théorème de Cayley.
Il est possible de prolonger ce morphisme. Soient K un corps commutatif, V un K-espace vectoriel de dimension g et B = (es) une base de V indexée par les éléments de G. L'action du groupe G précédente opère maintenant sur B. Si u est un élément de G, notons ρu l'application de B dans B qui à tout es, s dans G, associe l'élément eus. ρu opère sur une base de V. En conséquence, il est possible de prolonger ρu de manière unique comme une application linéaire de V dans V. Dorénavant, ρu désigne un endomorphisme de V. On remarque que l'image de la base B par ρu est encore une base, l'application ρ qui à u associe ρu est donc une application de G dans le groupe linéaire GL(V) des automorphismes de V.
Montrons que ρ est un morphisme de groupe, c’est-à-dire que :
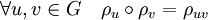
Il suffit pour cela, de vérifier l'égalité pour une base de V :
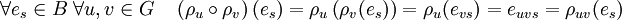
Ce qui permet la définition suivante :
-
- Soient u un élément de G et ρgu (resp. ρdu) l'unique application linéaire prolongeant l'action du groupe G à B par translation à gauche (resp. droite) sur V. Alors (V, ρg) (resp. V, ρd) est appelée représentation régulière à gauche (resp. droite) du groupe G.
Dans l'article la représentation est notée (V, ρ), les propriétés décrites sont vérifiées par les deux représentations droite et gauche. Un exemple est développé dans l'article Représentations du groupe symétrique d'indice trois.
Propriétés
Propriétés élémentaires
-
- Une représentation régulière est fidèle.
Dire qu'une représentation est fidèle, signifie qu'elle est injective. Pour montrer cette propriété, il suffit d'étudier le noyau de la représentation. soit s un élément du noyau, alors ρs est égal à l'identité. En particulier, l'image du vecteur de la base indexée par 1 est lui-même, donc s.1 = 1, et donc s = 1.
-
- Si χ désigne le caractère de la représentation régulière, alors χ1 = g et si s est un élément de G différent de 1, alors χs = 0.
En effet, considérons la matrice de ρs, c'est une matrice de permutation composée de zéro et de un. Une telle matrice possède un un sur la diagonale si et seulement s'il existe un élément t de G tel que ρs(et) = et, ce qui s'écrit encore st = t. La dernière égalité est impossible si s est différent de 1. χs = 0 est donc vérifiée si et seulement si s est différent de zéro. Le fait que χ1 = g, la dimension de V est une propriété générale à tous les caractères.
Nombre de représentations irréductibles
Si la caractéristique de K est nulle ou première avec g l'ordre du groupe et si le polynôme Xg - 1 est scindé dans K, alors les caractères irréductibles forment une base orthonormale des fonctions centrales, la démonstration est donnée dans l'article associé. On en déduit la proposition suivante :
-
- Soient (V, ρ) la représentation régulière de G et (W, σ) une représentation irréductible de G de degré d, il existe exactement d sous espaces invariants Vi de V, d'intersection nulle deux à deux, tel que la restriction ρi de ρ à Vi soit une représentation isomorphe à (W, σ).
Si ψ désigne le caractère de σ, on a alors:

Comme les caractères irréductibles forment une famille orthonormale, on en déduit la proposition.
Cette décomposition n'est pas unique. Le nombre de sous-espaces isomorphes à W de V est en général supérieur à d, mais ils ne sont pas en somme directe.
Cette propriété est utile, par exemple pour déterminer la table des caractère d'un groupe. Elle est utilisée par exemple pour établir cette table dans le cas du groupe alterné d'indice 5.
Identités remarquables
Le nombre de représentations irréductibles d'un groupe fini est fini. Soit h le nombre de représentations irréductibles distinctes de G, di le degré de la i-ième représentation irréductible de G et ψi son caractère, on a alors :
-
- Les deux égalités suivantes sont vérifiées :
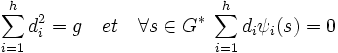
En effet, le théorème de Maschke montre que :
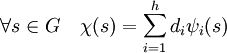
Cette égalité, limitée au cas ou s est égal à 1 donne :
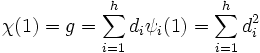
Dans le cas ou s est différent de 1, on obtient :
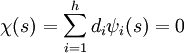
Algèbre d'un groupe
L'algèbre d'un groupe est un enrichissement algébrique de la représentation régulière. Ce n'est plus uniquement le groupe qui opère sur V, mais l'ensemble des combinaisons linéaires des éléments du groupe. L'ensemble qui opère sur V devient alors V lui-même. On obtient une algèbre associative sur K.
Cette algèbre est importante car le théorème de Maschke montre qu'elle est semi-simple. Or les algèbres semi-simples possèdent de nombreuses propriétés. On peut citer par exemple le fait qu'il existe une unique décomposition en composantes isotypiques, si (W, σ) désigne une représentation irréductible de G et (V, ρ) la représentation régulière, alors :
-
- Il existe un unique sous-espace maximal SW de V contentant tous les sous-espaces isomorphe à W. Il est appelé composante isotypique de W dans V. Les composantes isotypiques sont en somme directe égal à V.
Cette algèbre possède un centre disposant d'une structure d'anneau commutatif, il est ainsi possible d'utiliser les techniques de l'arithmétique et de démontrer que toute représentation irréductible possède un degré divisant celui de la représentation régulière.
Produit hermitien en caractéristique nulle
Si le corps K est de caractéristique nulle, comme il est commutatif, il est inclus dans C le corps des nombres complexes, l'espace V est naturellement munis de produit hermitien. Si K est inclus dans le corps des réels, alors le produit hermitien apparaît comme un produit scalaire.
-
- Soit ( | ) le produit hermitien conférant à la base canonique le statut de base orthonormale, ce produit hermitien est appelé produit hermitien canonique.
Tous les automorphismes images de la représentation ont pour image de la base canonique une base orthonormale, en effet la base de l'image est identique à la base canonique à une permutation près. Ils sont donc tous des isométries :
-
- Les images de la représentation régulière sont des automorphismes orthogonaux pour le produit hermitien canonique.
Une telle propriété induit la définition suivante :
-
- Un produit scalaire (ou hermitien) sur V est dit invariant par l'action de G si et seulement si l'image de G par ρ est composée d'isométries.
De plus, tout représentation irréductible est isomorphe à une sous-représentation de la représentation régulière. Il existe donc un produit hermitien ou scalaire invariant par l'action de G. Enfin, comme toute représentation est somme directe de représentations irréductibles :
-
- Si le corps K est de caractéristique nulle, toute représentation possède un produit hermitien ou scalaire invariant.
Produit hermitien en caractéristique finie
Dans le cas de la caractéristique finie, si le corps est algébrique et si la caractéristique p est première avec l'ordre g du groupe, alors la situation est analogue. Il est néanmoins nécessaire de définir un produit hermitien généralisé. Pour cela il faut exhiber une application équivalente à la fonction conjuguée des complexes. La théorie de Galois affirme l'existence d'un automorphisme de Frobenius φ vérifiant les propriétés suivantes :
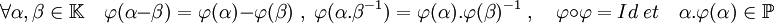
Le corps premier désigne le corps engendré par l'unité, il est isomorphe à Z/p.Z si p est la caractéristique de K. Si α est un élément non nul du corps, si d est le cardinal de la plus petite extension contenant α, alors φ(α)=αd/2. Les démonstrations sont données dans l'article Automorphisme de Frobenius. La forme hermitienne < | > possède les propriétés suivantes si φ(α) est noté
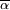
Cette généralisation ramène la situation au cas de caractéristique nulle, on en déduit la proposition :
-
- Si le corps K est de caractéristique finie première avec l'ordre du groupe et s'il est algébrique, toute représentation possède un produit hermitien invariant.






















































